约瑟夫问题

约瑟夫问题
苏丙榅1. 缘起
约瑟夫问题又叫约瑟夫环或丢手绢问题。故事据说发生在古罗马时期,在罗马人占领乔塔帕特后,39个犹太人与约瑟夫及他的朋友躲到一个洞中,他们宁愿死也不要被敌人抓到,于是约定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下1个人重新报数,直到所有人都自杀身亡为止。但是约瑟夫和他的朋友并不想死,就开始计算要站在什么地方才能避免被处决。
很显然如果想要逃避死亡,约瑟夫和他的朋友的死亡顺序应该是倒数第一和倒数第二,那么如何才能快速计算出这两个位置呢?

通过上图的推演大家应该是受到了启发,这个问题的本质其实就是循环链表的问题,围成一个圈之后,一个一个顺序报数,这就是相当于是在遍历循环链表。数到对应数字的出列,这就相当于是搜索并删除了循环链表中的一个节点!
2. 解决问题
既然处理约瑟夫问题需要用到循环链表,那么这个链表是选择带头结点的还是不带头结点的呢?
仔细分析之后相信大家选择的都是不带头结点的循环链表,因为现在的需求是通过最后一个数据节点直接找到链表中的第一个数据节点,如果是带头结点的循环链表,由于头结点不携带任何数据,在完成一轮遍历之后会对下一轮的衔接造成干扰(每次循环都需要跳过头结点)。
2.1 定义约瑟夫环类
在编写链表代码之前,我们先定义一个链表节点:
1 | struct Node |
在这个节点中一共有三个成员,它们的作用依次是:
data:存储数据pos:记录当前节点在链表中的位置(辅助调试用,可有可无)next:存储当前节点的后继节点的地址
在C++中,结构体就是类,所以给节点类提供了一个构造函数,通过构造函数的初始化列表来初始化构造函数的参数。
有了链表节点之后,就可以定义一个约瑟夫环类了,通过这个类来解决约瑟夫怎么活下来的问题:
1 |
|
在这个类中一共提供了3个函数:
- 构造函数:参数
size表示初始化到约瑟夫环中的元素数量- 随机生成
size个元素,并将他们串联成一个单向循环链表 - 这个单向循环链表没有头结点,只有数据节点
- 随机生成
- 遍历函数:通过
display函数遍历链表中的节点 - 幸存者函数:通过
findSurvivor函数计算约瑟夫环中的元素的死亡顺序- 参数
m表示数几个数死一个人
- 参数
2.2 实现约瑟夫环类
在这个类中的核心函数就是void findSurvivor(int m)函数,该函数的核心处理思想如下:
- 根据头指针从第一个数据节点开始向后遍历
- 每个节点从
1开报数,依次累加,数到m的节点需要从链表中删除 - 被删除的节点的后继节点重新从
1开始报数 - 重复第2、3步,直到链表为空终止循环
- 链表中节点被删除的顺序就是约瑟夫环中的人的死亡顺序
1 |
|
运行程序,终端输出的信息如下:
1 | 遍历约瑟夫环: |
我们可以根据节点在循环链表中的pos位置进行推导(从1号位开始),从1开始数,数到3的人出列(自杀),具体过程如下:
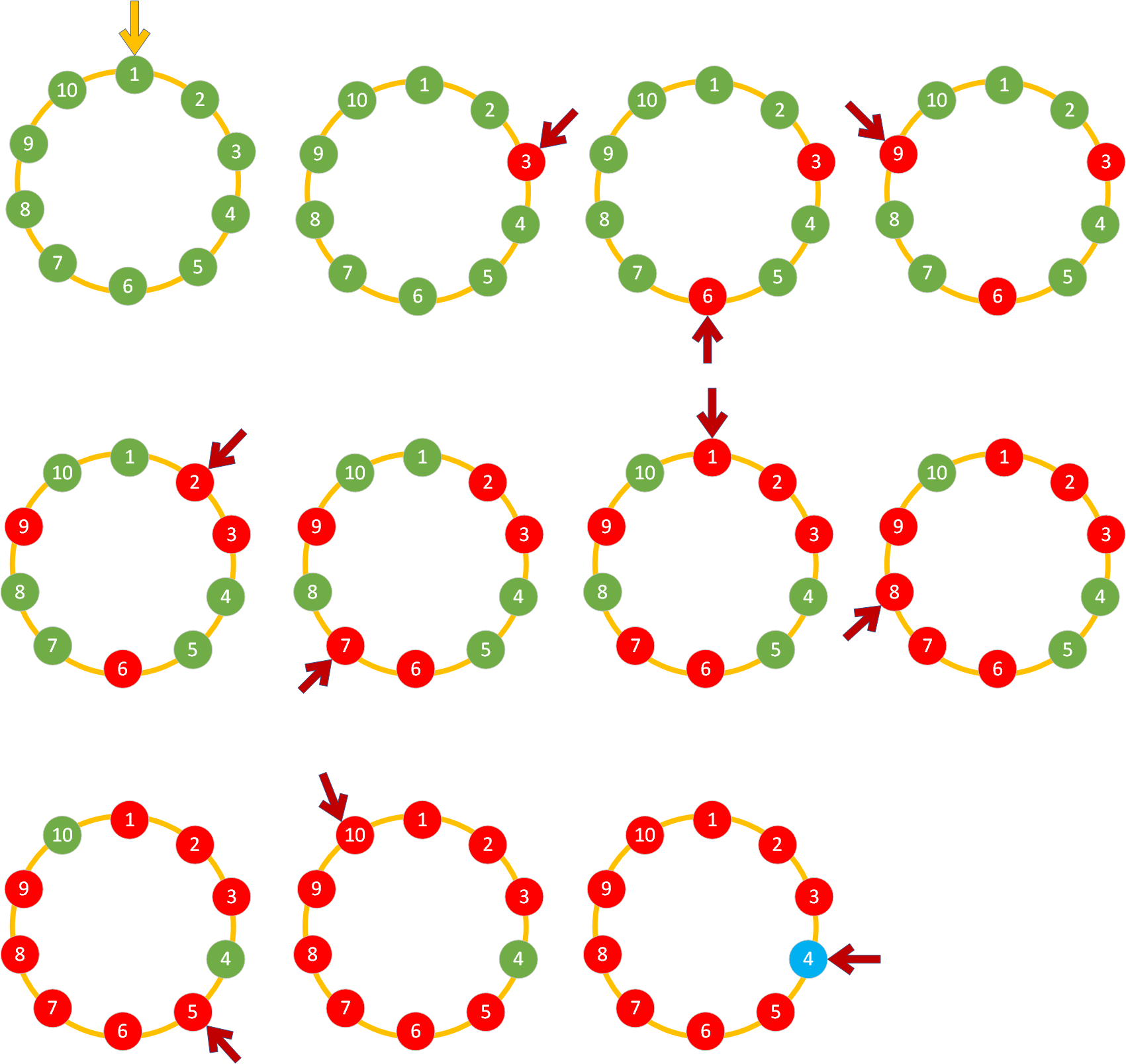
从图2开始,红色的箭头表示链表中当前出列(自杀)的节点,次序为:3,6,9,2,7,1,8,5,10,4。这个结果和程序打印出的次序是相同的。
所以,对于约瑟夫而言,如果有10个人,他和他的朋友需要分别站在4号位和10号位就可以活下来了。如果是上文所说的41个人,在程序中带入参数,得到的两个位置分别是16号位和31号位。
1 | 遍历约瑟夫环: |





















