线性表之数组

数组（Array）是 C/C++ 中最基础和重要的数据结构之一，它提供了一种有效存储和访问固定大小元素集合的方式。关于数组的定义和使用相信大家都已经熟练掌握，本文将着重为大家剖析数组的物理结构和逻辑结构。

1. 数组的物理结构

数组的物理结构是指数组元素在内存中的实际存储方式。在内存中，数组元素是连续存储的，这意味着相邻元素的地址是连续的，且每个元素占用固定大小的内存空间。

例如，对于一个整型数组 int numbers[5]，如果数组的起始地址为 0x1000，每个整型元素占据4个字节，那么数组中的元素在内存中的存储情况可能如下：

1
2
3
4
5
0x1000: numbers[0]
0x1004: numbers[1]
0x1008: numbers[2]
0x100C: numbers[3]
0x1010: numbers[4]

这样的存储方式保证了对数组元素的快速访问和遍历，因为可以通过计算地址偏移来访问数组中的任意元素。

2. 数组的逻辑结构

2.1 线性表

数组是一种线性数据结构，它由相同类型的元素组成，并以连续的内存地址存储。所谓的线性表就是由一个或多个元素组成的有序序列。在一个线性表中头部节点只有一个后继节点，尾部节点只有一个前驱节点，头部和尾部中间的节点分别有一个前驱节点，一个后继节点，如下图：

根据从前到后的顺序，我们就可以将A1记作头结点，A5记作尾节点，A2~A4记作中间节点。拿A3举例，它的前驱节点是A2，后继节点是A4。

在逻辑上，数组是一个有序集合，每个元素可以通过唯一的下标（索引）来访问。

例如，数组 int numbers[5] 中的元素可以用 numbers[0]、numbers[1]、numbers[2]、numbers[3] 和 numbers[4] 这些下标来访问。这种抽象方式隐藏了数组元素在内存中的实际存储方式，使程序员只需关注元素的逻辑位置而无需担心其物理存储。

2.2 数组的优缺点

关于数组的使用，它的优缺点总结如下：

  • 优点
    • 通过下标访问数组中的任意元素速度非常快，时间复杂度是 O(1)
    • 末尾位置增加、删除元素速度非常快，时间复杂度是O(1)
    • 访问当前元素前、后相邻位置的元素非常方便
  • 缺点
    • 非末尾位置增加、删除元素需要进行大量的数据移动，时间复杂度为 O(n)
    • 搜索效率比较低，时间复杂度
      • 无序数组 - 线性搜索 O(n)
      • 有序数组 - 二分搜索O(logn)
    • 数组扩容的时候资源开销比较大

2.3 动态数组

在C语言中是没有动态数组的概念的，只有静态数组。想要使用动态数组只能由程序员自己实现，其核心思想有以下几点：

  1. 记录下数组的容量和数组中存储的数据的个数
  2. 当数组的容量 == 存储的数据个数的时候重新申请一块新内存或者扩容
    • 可以使用realloc（函数位于第3章）对数组进行扩容
    • 可以使用new或者malloc重新申请一块更大的内存，然后再将旧数据拷贝到新内存中，最后释放旧的内存资源

与此同时，如果要求这个动态数组可以在不同场景下存储不同类型的数据，我们就需要使用泛型编程，因此可以这样定义这个类:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
using namespace std;

template <typename T>
class Array
{
public:
    Array(int size = 64);
    ~Array();

    // 在尾部添加元素
    void append(T val);
    // 尾部删除元素
    void popBack();
    // 插入元素
    void insert(int pos, T val);
    // 删除元素
    void remove(int pos);
    // 查询元素-> 返回位置
    int find(T val);
    // 得到指定位置的元素的值
    int value(int pos);
    // 获取数组元素数量
    int size();
    // 打印数据
    void show();
private:
    void expand(int size);
private:
    T* m_arry;           // 数组的起始地址
    int m_capacity;      // 数组容量
    int m_count;         // 数组中的元素数量
};

在编写模板类的时候需要注意一个问题：类的声明和定义要写到同一个文件中，如果分开写到 .h 和 .cpp 中，编译的时候就会出现链接错误。因此在实现上边这个的类的时候可以将代码写到一个 .h 或者 .hpp 文件中。

array.hpp 文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
#include <iostream>
#include <cassert>
using namespace std;

template <typename T>
class Array
{
public:
    Array(int size = 64);
    ~Array();

    // 在尾部添加元素
    void append(T val);
    // 尾部删除元素
    void popBack();
    // 插入元素
    void insert(int pos, T val);
    // 删除元素
    void remove(int pos);
    // 查询元素-> 返回位置
    int find(T val);
    // 得到指定位置的元素的值
    int value(int pos);
    // 获取数组元素数量
    int size();
    // 打印数据
    void show();

private:
    void expand(int size);

private:
    T* m_arry;           // 数组的起始地址
    int m_capacity;      // 数组容量
    int m_count;         // 数组中的元素数量
};

template <typename T>
Array<T>::Array(int size) :
    m_capacity(size),
    m_count(0),
    m_arry(new T[size]()) 
{
}

template <typename T>
Array<T>::~Array()
{
    // 释放资源
    delete[]m_arry;
    m_arry = nullptr;
}

template <typename T>
void Array<T>::append(T val)
{
    // 满了, 扩容
    if (m_count == m_capacity)
    {
        expand(m_capacity * 2);
    }
    m_arry[m_count++] = val;
}

template <typename T>
void Array<T>::popBack()
{
    if (m_count == 0)
    {
        return;
    }
    m_count--;  // 把尾部元素变成了无效元素
}

template <typename T>
void Array<T>::insert(int pos, T val)
{
    if (pos < 0 || pos > m_count) 
    {
        cout << "插入数据失败: 无效的pos位置" << endl;
        return;
    }
    if (m_count == m_capacity)
    {
        expand(2 * m_capacity);
    }
    // 移动元素
    for (int i = m_count - 1; i >= pos; --i)
    {
        m_arry[i + 1] = m_arry[i];
    }
    m_arry[pos] = val;
    m_count++;
}

template <typename T>
void Array<T>::remove(int pos)
{
    if (pos < 0 || pos >= m_count)  
    {
        return;
    }
    int value = m_arry[pos];
    for (int i = pos + 1; i < m_count; ++i)
    {
        m_arry[i - 1] = m_arry[i];
    }
    m_count--;
}

template <typename T>
int Array<T>::find(T val)
{
    for (int i = 0; i < m_count; ++i)
    {
        if (m_arry[i] == val)
        {
            return i;
        }
    }
    return -1;
}

template<typename T>
int Array<T>::value(int pos)
{
    assert(pos >= 0 && pos < m_count);
    return m_arry[pos];
}

template<typename T>
int Array<T>::size()
{
    return m_count;
}

template <typename T>
void Array<T>::show()
{
    for (int i = 0; i < m_count; ++i)
    {
        cout << m_arry[i] << " ";
        cout << (int)m_arry[i] << " ";
    }
    cout << endl;
}

template <typename T>
void Array<T>::expand(int size)
{
    // 申请一块新的内存
    T* ptr = new T[size]();
    // 旧数据拷贝到新内存
    memcpy(ptr, m_arry, sizeof(T) * m_capacity);
    delete[]m_arry;
    // 数据更新
    m_arry = ptr;
    m_capacity = size;
}

上面的代码是通过append或者insert函数往数组中添加数据的时候，判断了数组中已存储的元素数量，如果数组已满便调用expand函数进行扩容。

  • 使用relloc函数扩容比重新分配内存的方式要简单一些，如果它在其它位置开辟了新的存储空间而不是在尾部扩容，会自动释放旧的内存块。
  • 对数组进行动态扩容之后，要对数组的容量进行更新。
  • 对数组进行动态扩容之后，要更新数组指针指向的起始地址。

另外，通过阅读上述代码也可以证明在数组的中间位置添加、删除数据都会涉及到元素的大量移动（后移或者前移），操作相率相对较低。

3.案例

数组作为 C/C++ 程序员密不可分的战友，其重要性在此不再过多赘述，下面有两个算法题，大家来一起练练手。

3.1 元素逆序

将数组中的所有元素首尾调换位置，假设数组中有N个元素：

  • 0号 和 N-1 号 元素调换位置
  • 1号 和 N-2 号 元素调换位置
  • 2号 和 N-3 号 元素调换位置
  • ……

比如原始序列为：1、2、3、4、5、6、7、8、9

处理完之后的序列应该为：9、8、7、6、5、4、3、2、1

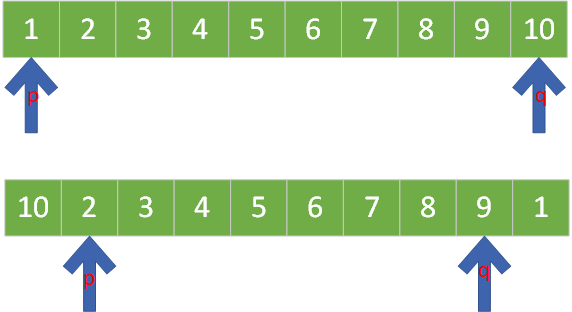
要解决这个问题需要使用辅助指针，因为是需要交换数组中前后元素的位置，所以辅助指针需要两个，一个从数组头部开始，一个从数组尾部开始：

  • 数组头部元素位置的下标为：0
  • 数组尾部的元素位置的下标为：数组元素数量 - 1

两个辅助指针同时移动，这样当两个指针相遇的时候，数组中所有元素的交换也就完成了，如下图：

根据上面的分析，可以在前面的Array模板类中添加一个反转函数:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
template<typename T>
void Array<T>::reverse()
{
    T* p = m_arry;                  // 头部
    T* q = m_arry + m_count - 1;    // 尾部
    while (p < q)
    {
        T tmp = *p;
        *p = *q;
        *q = tmp;
        p++;
        q--;
    }
}

处理该问题的核心思想就是使用双辅助指针，然后同时移动这两个指针，并完成元素的交换，这样就可事半功倍。

3.2 奇偶调整

将一个整形数组中的数据进行调整：

  • 把所有的奇数放到数组的左侧
  • 把所有的偶数放到数组的右侧

这个题目可以理解为是上个题目的升级版，我们来说具体分析一下：

  • 奇数和偶数需要分别放在数组的两侧，所以需要的辅助指针有两个
  • 两个指针一前一后各自对指向的当前元素进行奇偶判断，常用的判断奇偶的方式有两种：
    • 对数据进行number%2操作，结果为0是偶数，否则是奇数
    • 对数据进行number&1 操作，结果为0是偶数，否则是奇数
  • 循环执行第二步，当找到了不满足条件的元素之后，交换前后两个指针指向的元素的值
  • 当前后两个指针相遇的时候，数组中的数据调整完毕。

根据上面的分析，还是在Array模板类中添加一个处理函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
template<typename T>
void Array<T>::adjust()
{
    T* p = m_arry;                  // 头部
    T* q = m_arry + m_count - 1;    // 尾部
    while (p < q)
    {
        while (p < q) 
        {
            if ((*p & 1) == 0)
            {
                break;
            }
            p++;
        }
        while (p < q)
        {
            if ((*q & 1) == 1)
            {
                break;
            }
            q--;
        }
        // 数据交换
        if (p < q)
        {
            T tmp = *p;
            *p = *q;
            *q = tmp;
            p++;
            q--;
        }
    }
}
  • 第 6 行的 while (p < q)循环表示前后奇偶数交换还未完成，继续对数组进行遍历
  • 第 8 行的 while (p < q)循环表示如果当前元素是奇数，当前指针继续后移
  • 第 16 行的 while (p < q)循环表示如果当前元素是偶数，当前指针继续前移
  • 第 10 行的if ((*p & 1) == 0)判断表示在数组前半部分找到了偶数
  • 第 18 行的if ((*q & 1) == 1)判断表示在数组后半部分找到了奇数