线性表之串和朴素模式匹配算法

线性表之串和朴素模式匹配算法
苏丙榅1. 串
“天行健,君子一自强不息;地势坤,君子以厚德载物”这是《易经》中的原文,对于普通人而言这就是两句话,对于程序员来说这就是一个数据块,是多个相同类型的字符的集合,在数据结构中将其称之为串。
串(String)是由零个或多个字符组成的有限序列,又名叫字符串。一般记作 s=“a1a2a3……an” (n>=0)。其中,s是串的名称,双引号(或单引号)括起来的字符序列是串的值,但是要注意引号不属于串的内容。
空串:零个字符的串成为空串,它的长度为0,可以用双引号“”表示串的长度:串中的字符的数量就是串的总长度
1.1 串的储存结构
串的存储结构和线性表相同,分为两种顺序存储结构和链式存储结构。
顺序存储结构:
串的顺序存储结构是用一组地址连续的存储单元(说白了
就是数组)来存储串中的字符序列。大家都学过C语言,此处就不再展开阐述了。
链式存储结构:
对于串的链式存储结构,与线性表相似,但由于串结构的特殊性,结构中的每一个数据元素是一个字符,那么一个链表节点存储一个字符就存在很大的空间浪费,因此可以考虑使用一个节点存储多个字符,最后一个节点如果没有被占满,可以使用一些事先约定好的特殊字符来填充,比如
#当然,链表中一个节点存储多少个字符才合适就变得很重要,这会直接影响到串的处理效率,需要根据实际情况做出选择。
串的链式存储结构除了在连接两个串时比较方便之外,总的来说不如顺序存储结构灵活,性能也不如顺序存储结构好。
1.2 串的比较
串的比较通常是字典序比较。字典序比较指的是按照字典(词典)中的顺序来比较字符串或者其他可比较的数据类型。在字典序中,比较的依据是从左到右逐个字符比较它们的Unicode码点(字符编码),直到找到两者之间的差异为止。
具体来说,对于两个字符串的比较,会按照它们的第一个字符进行比较。如果第一个字符相同,则比较第二个字符,依此类推,直到找到不同的字符或者其中一个字符串结束。比较时遵循字符的Unicode码点大小关系,例如: ‘A’ < ‘B’ < … < ‘Z’ < ‘a’ < ‘b’ < … < ‘z’ 。
字典序比较不仅仅用于字符串,也可以用于比较数字、日期等数据类型,遵循类似的规则。
例如,对于字符串 “apple” 和 “banana”:
按字典序比较,首先比较 ‘a’ 和 ‘b’,‘a’ 小于 ‘b’,因此 “apple” < “banana”。
字典序比较在排序、搜索、数据库操作等场景中非常常见,因为它提供了一种直观的排序和查找方式,符合人们日常生活中字典的排列方式。
最后,我们来总结一下比较两个串 ( S ) 和 ( T ) 的具体过程:
- 从第一个字符开始逐个比较。
- 如果 (
s_i < t_i),则 (S < T)。 - 如果 (
s_i > t_i),则 (S > T)。 - 如果 (
s_i = t_i),则继续比较下一字符,直到一个串结束。- 如果一个串先结束,则短串更小。
- 如果两个串长度相同且所有字符都相同,则两个串相等。
2. 朴素的模式匹配算法
在我们拿到一篇文章或者一个长的数据块的时候,很多时候都需要去里边搜索一些关键字或者短句,这种字串的定位操作通常称作串的模式匹配。
朴素的模式匹配算法(Naive Pattern Matching Algorithm)是最简单的字符串匹配算法。其基本思想是从主串的每一个位置开始,尝试匹配模式串,直到找到匹配或搜索完毕。
朴素的模式匹配算法主要分为两个阶段:匹配阶段和移动阶段。
匹配阶段
从文本的第一个字符开始:将模式字符串与文本字符串的每一个可能的起始位置进行比较。
逐个比较字符:从文本的当前位置和模式的第一个字符开始,逐个比较两个字符串的字符是否相同。
匹配成功:如果当前字符匹配,则继续比较下一个字符,直到模式字符串全部匹配完成。
匹配失败:如果有字符不匹配,则停止当前位置的匹配,将模式字符串向后移动一个位置,重新从文本的下一个位置开始比较。
移动阶段
模式字符串向后移动:如果在当前位置匹配失败,将模式字符串向右移动一个位置,重新开始匹配过程。
重复比较:重复以上过程,直到找到匹配或者模式字符串的末尾超出文本的末尾。
比如,现在有一个原始字符串
dadadabing,想要从里边搜索子字符串dabing,使用朴素的模式匹配算法对应的匹配过程如下:
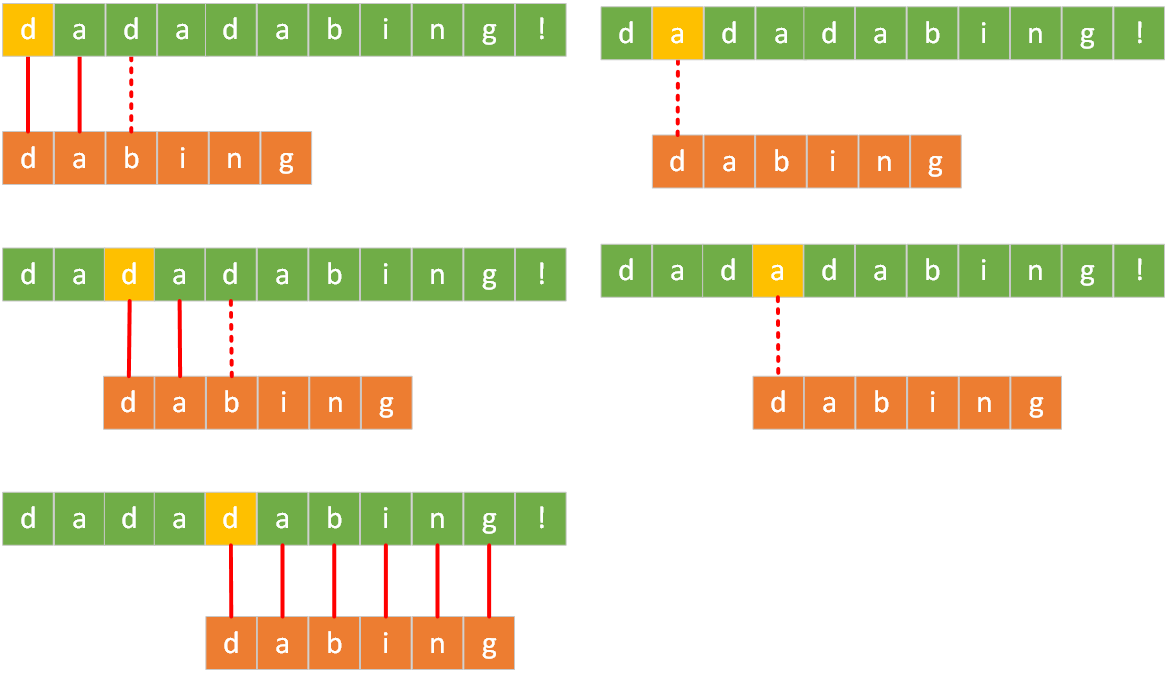
根据描述我们就可以使用朴素的模式匹配算法写出对应的C++代码了:
1 |
|
朴素的模式匹配算法的优缺点都非常明显,优点是简单很容易理解,缺点是搜索效率低(时间复杂度为 O(n*m)),关于朴素模式匹配算法效率低的原因我们来简单的分析一下:
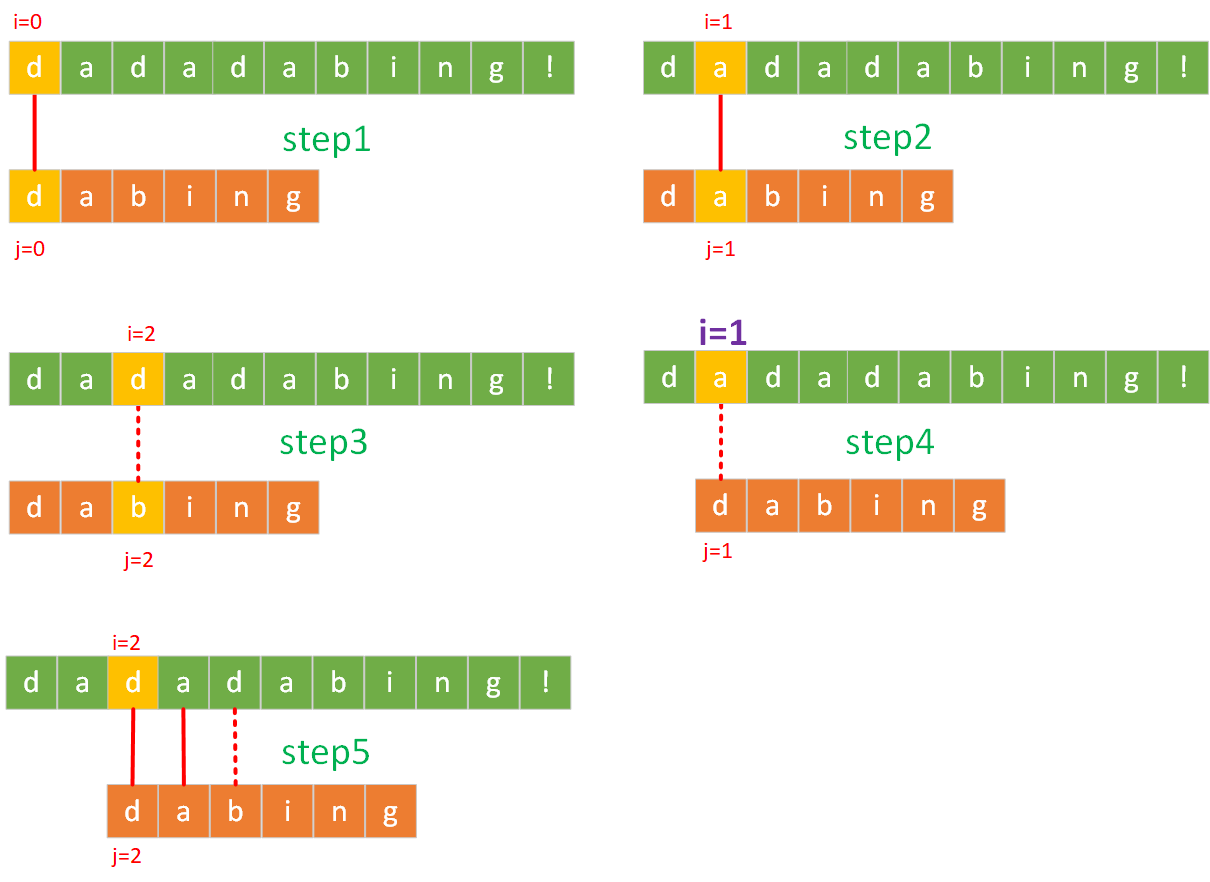
在上图中为大家展示了主串和模式串的部分匹配过程,我们来看一下其中的细节:在模式串中字符d和字符a是不相等的,所以模式串中的d和主串中的a也是不相等的,因此可以得出如下结论:
step4的比较是多余的,可以直接从step3跳到step5,减少匹配次数- 在匹配过程中,保持主串匹配位置(
i)不回退,可提高匹配效率
如果数据量非常大,在搜索的时候使用这种算法就不合适了。如果需要提高效率,可以使用更高级的匹配算法KMP模式匹配算法























