线性表之栈

苏丙榅2024-06-242024-06-29

1. 栈

1.1 栈的由来

对于大多数人而言都对生活充满了热爱，如果对身边接触到的各种事物仔细观察就会发现它们有很多相似的特性：

给子弹上弹夹，先压进去的最后被发射出来，最后压进去的第一个被发射出来。
浏览器的后退键，第一次后退看到的是最后浏览的页面，最后一次后退看到的是第一次浏览的页面
带编辑功能的软件，比如：Office、Photoshop、IDE，第一次撤销得到的最后一次修改的内容，最后一次撤销得到的是第一次修改的内容

如果在以上的某一个场景下进行连续的操作，按照线性表的描述我们就可以得到一个从前到后的序列，并且在访问序列中的元素的时候是按照从后往前的顺序进行的。

如果对线性表中元素的访问进行了限制，那么这个线性表就被称作受限制的线性表。常用的受限制的线性表有栈和队列。

栈（Stack）是一种常见的数据结构，它遵循后进先出（Last In First Out，LIFO）的原则，即最新添加的元素最先被移除，也就是它要求仅能在表尾进行元素的插入和删除。

关于栈有几个相关的概念需要大家掌握：

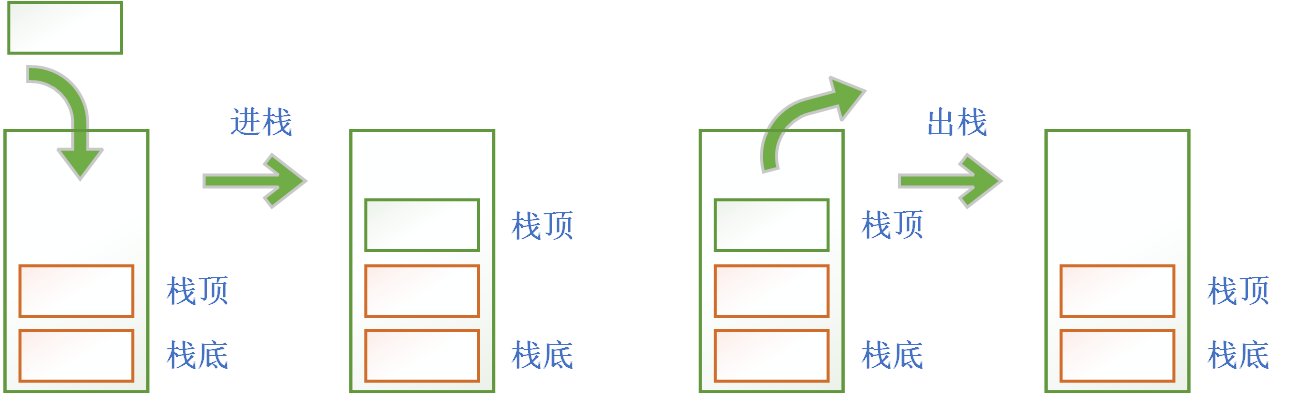
栈顶: 线性表允许插入、删除的一端被称为栈顶
栈底: 线性表不允许插入、删除的一端被称为栈底
压栈: 将数据添加到栈顶，也叫进栈、入栈
弹栈: 将数据从栈顶删除，也叫出栈
空栈: 不含任何元素的栈叫做空栈

1.2 栈的存储结构

因为线性表有两种存储结构顺序存储结构和链式存储结构，所以对于栈而言也有两种存储结构，分别是顺序栈和链式栈。

顺序栈：
- 基于数组实现，具有固定的大小。
- 优点是实现简单，访问元素速度快，但需要预先知道栈的最大容量。
链式栈：
- 基于链表实现（使用单向链表即可），没有固定大小限制，可以动态扩展。
- 优点是可以灵活地处理大小变化，但实现相对复杂，且在链表节点上有额外的内存开销。

2. 顺序栈

2.1 栈顶在哪儿?

前面也说到了，顺序栈是通过数组来实现的，假设我们要存储整形数据，那么在实现顺序栈的时候，准备一个整形数组即可。

根据栈的特性，只能对栈顶进行操作，那么对于数组而言栈顶在哪儿呢？有两种解决方案，下面我们来一起分析一下它们的可行性：

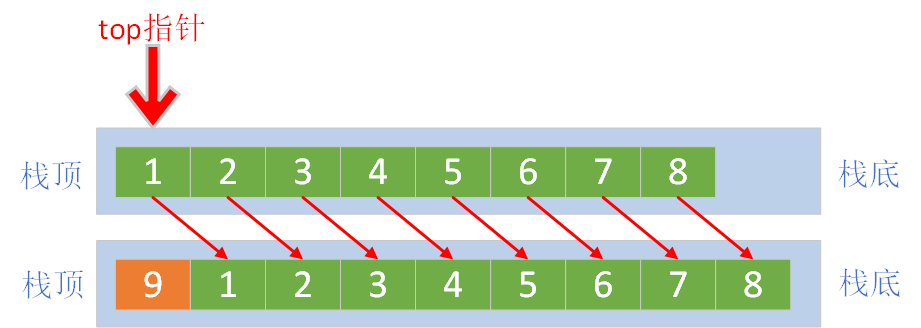
数组的头部做栈顶，尾部做栈底
- 入栈：每次入栈数组中所有的旧元素需要后移，时间复杂度O(n)
  
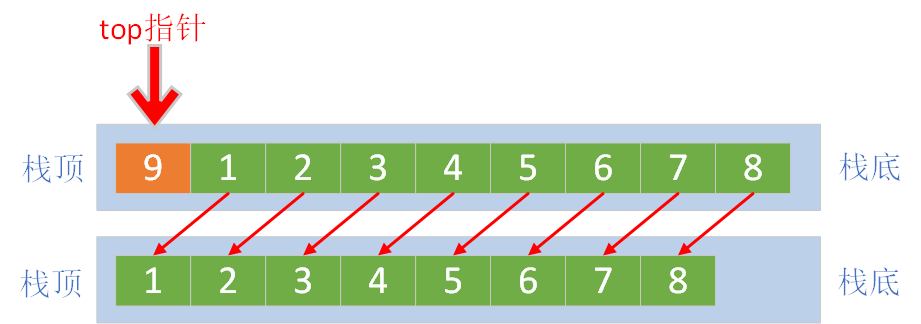
  上图的入栈顺序为8、7、6、5、4、3、2、1、9
- 出栈：每次出栈数组中所有的剩余元素需要前移，时间复杂度O(n)
  
  上图的出栈顺序为9、1、2、3、4、5、6、7、8
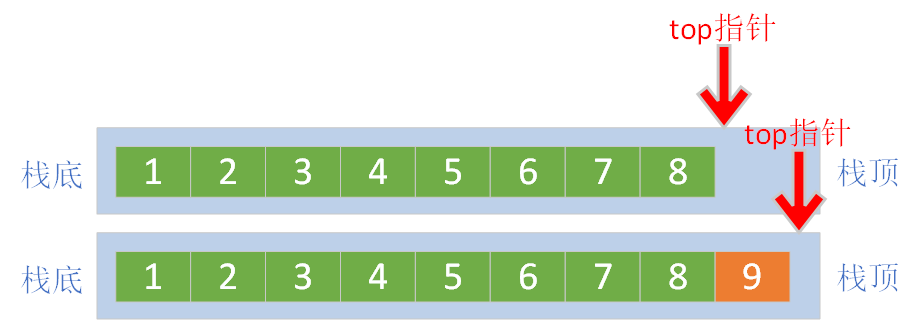
数组的尾部做栈顶，头部做栈底
- 入栈：直接将数据添加到数组尾部，不涉及到元素移动，时间复杂度O(1)
  
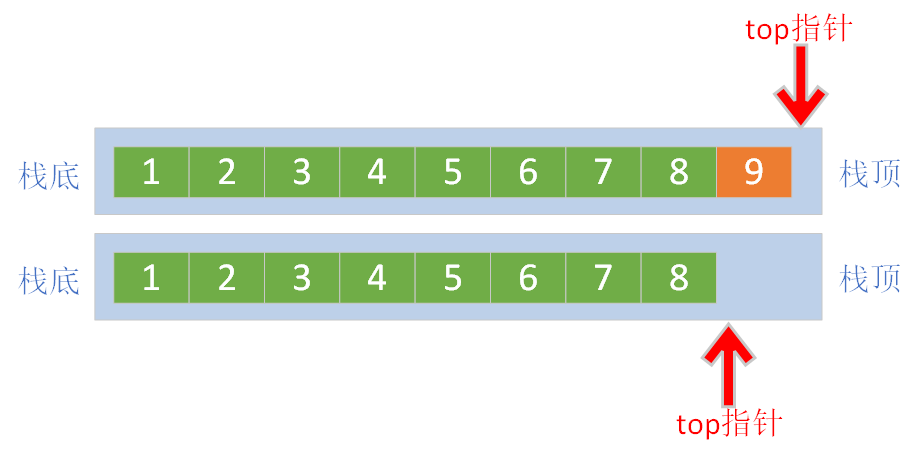
  上图的入栈顺序为1、2、3、4、5、6、7、8、9
- 出栈：直接将数据从数组尾部删除，不涉及到元素移动，时间复杂度O(1)
  
  上图的出栈顺序为9、8、7、6、5、4、3、2、1
所以现在可以得到一个结论：如果是顺序栈，选择数组的尾部作为栈顶，操作效率是最高的，时间复杂度为 O(1)。

2.2 顺序栈的实现

我们先定义一个C++的类，来实现这个顺序栈。

头文件

// ArrayStack.h
#pragma once
const int MAX_SIZE = 100;

class ArrayStack 
{
public:
    ArrayStack();
    bool isEmpty();
    bool isFull();
    // 压栈
    void push(int x); 
    // 出栈
    int pop();
    // 得到栈顶元素
    int top();
private:
    int m_data[MAX_SIZE];
    int m_top;
};

const int MAX_SIZE = 100：整形常量，设置栈的最大容量为100
int m_top：类的私有成员，栈顶指针，用来描述可存储数据的栈顶元素在数组中的位置（数组末尾元素的下一个位置）。

源文件

// ArrayStack.cpp
#include <iostream>
#include "ArrayStack.h"
using namespace std;

ArrayStack::ArrayStack() : m_top(0) {}

bool ArrayStack::isEmpty() 
{
    return m_top == 0;
}

bool ArrayStack::isFull() 
{
    return m_top == MAX_SIZE;
}

void ArrayStack::push(int x) 
{
    if (isFull()) 
    {
        cout << "栈已经满了, 数据无法入栈!" << endl;
        return;
    }
    m_data[m_top++] = x;
}

int ArrayStack::pop() 
{
    if (isEmpty()) 
    {
        cout << "空栈, 无法弹出元素!" << endl;
        return -1;
    }
    return m_data[--m_top];
}

int ArrayStack::top() 
{
    if (isEmpty()) 
    {
        cout << "空栈, 无法访问栈顶元素!" << endl;
        return -1;
    }
    return m_data[m_top - 1];
}

int main() 
{
    ArrayStack stack;
    stack.push(1);
    stack.push(2);
    stack.push(3);
    cout << "栈顶元素: " << stack.top() << endl;
    stack.pop();
    cout << "新的栈顶元素: " << stack.top() << endl; 
    return 0;
}

通过代码可以看到顺序栈的实现是非常简单的，其实就是对数组的操作位置和操作方式进行了限制，通过选择合适的栈顶位置，提高了栈的工作效率。

在动态数组章节中，有关于对静态数组扩容的解决方案，感兴趣的小伙伴可以去考古。

3. 链式栈

3.1 栈顶怎么选？

链式栈的本质其实就是一个链表，链表和数组一样也是有头有尾的，那么选择哪一端作为链式栈的栈顶呢？下面我们来分析一下：

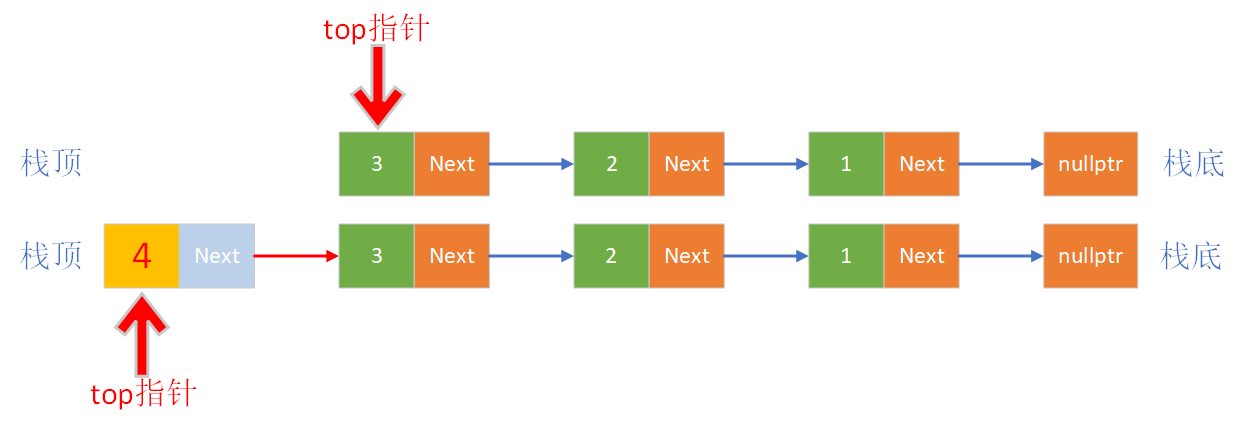
选择链表头部做栈顶，尾部做栈底
- 入栈：直接通过头指针可以找到头结点，在链表头部插入数据不涉及元素的遍历和移动，时间复杂度为O(1)
- 出栈：直接通过头指针可以找到头结点，在链表头部删除数据不涉及元素的遍历和移动，时间复杂度为O(1)
选择链表尾部做栈顶，头部做栈底
- 入栈：如果链表中没有维护尾指针，需要通过头指针对链表进行遍历，找到尾节点，完成新节点的尾部插入
  - 如果链表中有尾指针：可以直接找到链表尾节点，时间复杂度O(1)
  - 如果链表中没有尾指针：需要遍历链表找到尾节点，时间复杂度O(n)
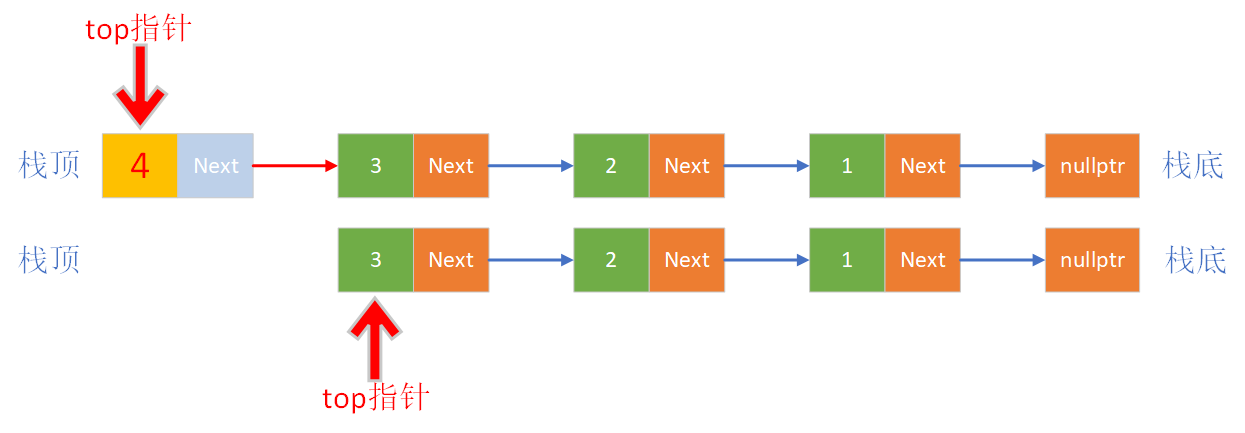
- 出栈：如果链表中没有维护尾指针，需要通过头指针对链表进行遍历，找到尾节点，完成对尾部节点的删除
  - 如果链表中有尾指针：可以直接找到链表尾节点，时间复杂度O(1)
  - 如果链表中没有尾指针：需要遍历链表找到尾节点，时间复杂度O(n)

通过以上描述可以得出结论：链式栈选择链表的头部作为栈顶处理起来最方便，效率也高。由于栈的特性，选择不带头结点的链表，可以让编写的链式栈更精简。

3.2 链式栈的实现

我们先定义一个C++的类，来实现这个链式栈。链式栈的本质是链表，根据栈的特性，选择链表中最简单的单向链表就足够满足需求了。

头文件

// LinkedStack.h
#pragma once
struct Node 
{
    int data;
    Node* next;
    Node(int d) : data(d), next(nullptr) {}
};

class LinkedStack 
{
public:
    LinkedStack();
    ~LinkedStack();
    bool isEmpty();
    void push(int x);
    int pop();
    int top();
private:
    Node* m_top;  // 栈顶指针，指向链表的头部
};

在这个链式栈的类中有一个私有成员Node* m_top，它代表栈顶指针，也就是链表的头指针，指向链表的头结点（如果是不带头结点的链表，那么此处的头结点指的就是它的第一个数据节点）。

源文件

// LinkedStack.cpp
#include <iostream>
#include "LinkedStack.h"
using namespace std;

LinkedStack::LinkedStack() : m_top(nullptr) {}

LinkedStack::~LinkedStack() 
{
    while (m_top != nullptr)
    {
        Node* temp = m_top;
        m_top = m_top->next;
        delete temp;
    }
}

bool LinkedStack::isEmpty() 
{
    return m_top == nullptr;
}

void LinkedStack::push(int x) 
{
    Node* newNode = new Node(x);
    newNode->next = m_top;
    m_top = newNode;
}

int LinkedStack::pop() 
{
    if (isEmpty()) 
    {
        cout << "空栈, 无法弹出元素!" << endl;
        return -1;
    }
    Node* temp = m_top;
    int value = temp->data;
    m_top = m_top->next;
    delete temp;
    return value;
}

int LinkedStack::top() 
{
    if (isEmpty()) 
    {
        cout << "空栈, 无法访问栈顶元素!" << endl;
        return -1;
    }
    return m_top->data;
}

int main()
{
    LinkedStack stack;
    stack.push(1);
    stack.push(2);
    stack.push(3);
    cout << "栈顶元素: " << stack.top() << endl;
    stack.pop();
    cout << "新的栈顶元素: " << stack.top() << endl;
    return 0;
}