线性表之队列

1. 队列

1.1 队列的由来

关于常用的受限制的线性表除了栈还有队列。队列与我们的日常生活息息相关，无时无刻都能感受到队列的存在：

  1. 早晨起床排队上厕所、洗漱
  2. 排队坐地铁、公交上下班，开车也需要排队通过交通路口
  3. 排队买早餐，排队在收银口结账，去热门餐厅吃大餐人多还得排队

建设文明和谐的社会需要队列，先进先出、先到先得这是一种公平的体现。由此可见栈、队列都是从日常生活中提炼出的结构化模型，是智慧的结晶。

队列（Queue）作为一种常见的数据结构，遵循先进先出（First In First Out, FIFO）的原则，即最早进入队列的元素最先被移除。队列广泛应用于缓冲区管理、任务调度、消息队列等场景。

和栈一样，队列中也有几个概念需要大家掌握：

  1. 队头: 线性表中允许删除数据的一端称为队头
  2. 队尾: 线性表中允许插入数据的一端称为队尾
  3. 入队列: 将元素添加到队尾的动作叫做入队列
  4. 出队列: 将元素从队头删除的动作叫做出队列
  5. 空队列: 没有存储任何元素的队列叫空队列，即该线性表是空的

1.2 队列的存储结构

因为线性表有两种存储结构顺序存储结构和链式存储结构，所以对于队列而言也有两种存储结构，分别是顺序队列和链式队列。而顺序队列又可以进行细分，又得到两种队列：非循环队列和循环队列。

  • 顺序队列：
    • 基于数组实现，具有固定的大小。
    • 优点是实现简单，访问元素速度快，但需要预先知道队列的最大容量。
  • 链式队列：
    • 基于链表实现，没有固定大小限制，可以动态扩展。
    • 优点是可以灵活地处理大小变化，但实现相对复杂，且在链表节点上有额外的内存开销

1.3 谁是队头谁是队尾?

队列和栈有很大的不同，栈只能对线性表的一端进行操作也就是栈顶。但是队列操作的是线性表的两端，如果确定了一端作为队头，那么另外一端就是队尾。

  • 顺序非循环队列

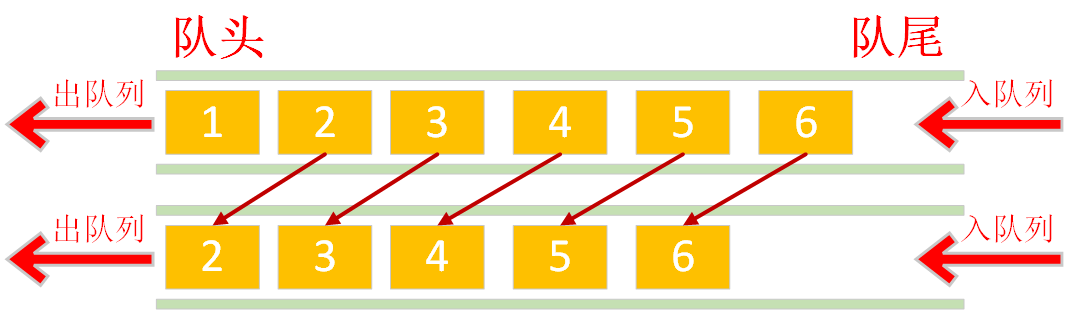
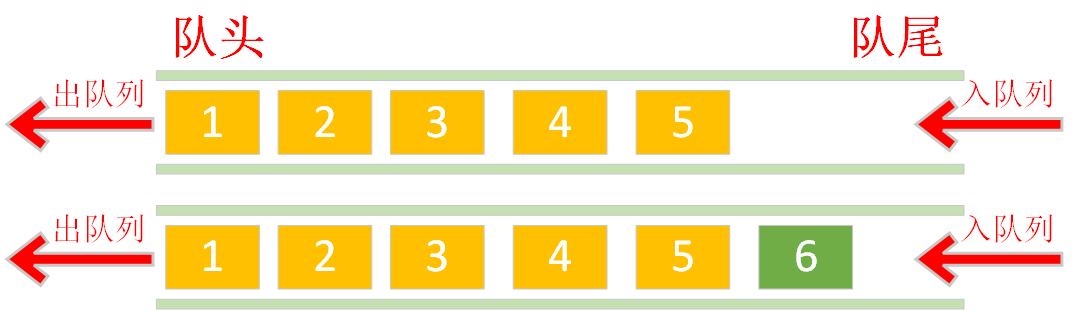
    • 数组的头部作为队头，数组的尾部作为队尾

      • 出队列：涉及到元素的大量前移，时间复杂度为O(n）

      • 入队列：不涉及到元素移动，直接把数据追加到队尾即可，时间复杂度O(1)

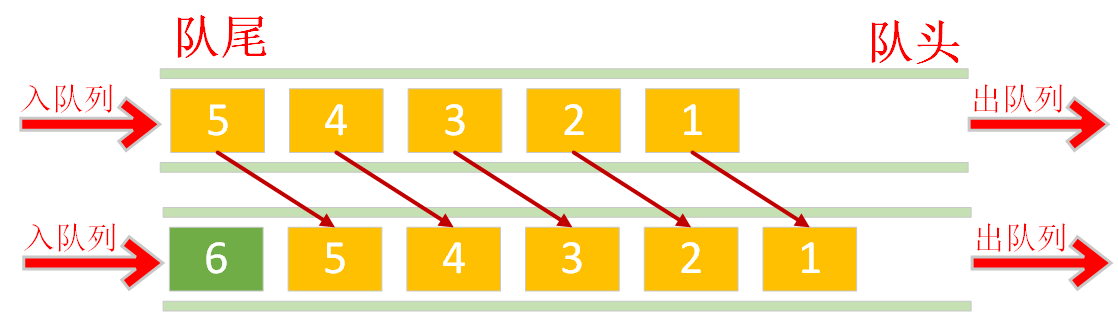
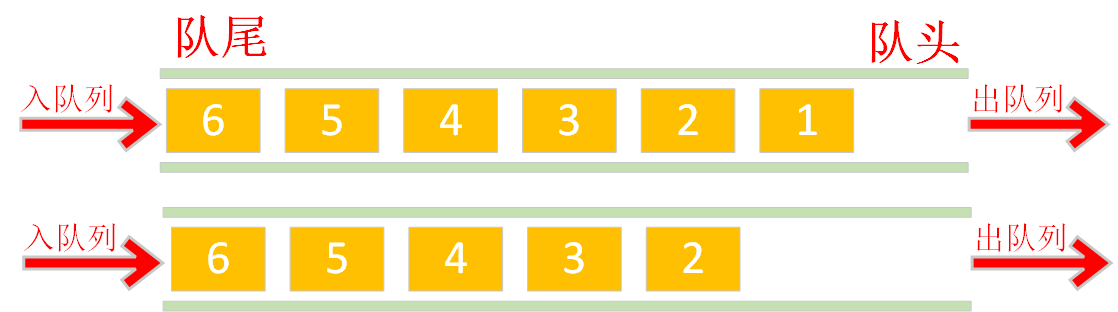
    • 数组的头部作为队尾，数组的尾部作为队头

      • 入队列：涉及到元素的大量后移，时间复杂度为O(n）

      • 出队列：不涉及到元素移动，直接把队尾数据删除即可，时间复杂度O(1)

    通过上面的分析可以得到一个结论：对于顺序非循环队列而言，无论是哪端作为队头，哪端作为队尾，在进行插入或者删除操作的时候其中一个都无法避免数组中的元素移动。在这种情况下随便选择一端作为队头或者队尾就可以了。

  • 链式队列

    • 链表头部作为队头，链表尾部作为队尾
      • 入队列:
        • 链表中有尾指针：可直找到尾节点，在队尾添加数据，时间复杂度为O(1)
        • 链表中没有尾指针：需要遍历链表找到尾节点，然后在队尾添加数据，时间复杂度为O(n)
      • 出队列：通过头指针可以直接找到头结点进行头部数据删除，时间复杂度为O(1)
    • 链表头部作为队尾，链表尾部作为队头
      • 入队列：通过头指针可以直接找到头结点（队尾）进行数据插入，时间复杂度为O(1)
      • 出队列：
        • 链表中有尾指针：可直找到尾节点，将链表尾部（队头）数据删除，时间复杂度为O(1)
        • 链表中没有尾指针：需要遍历链表找到尾节点，然后再将尾部（队头）数据删除，时间复杂度为O(n)

    所以，通过上面的分析可以得到如下结论：对于链式队列而言，链表的哪端作为队头，哪端作为队尾都是可以的，效率上没有差别。

2. 顺序非循环队列

顺序非循环队列一般被我们简称为顺序队列。它的本质就是一个数组，既然是非循环所以它的首尾是不相接的，我们还是先定义一个C++类，来实现这个顺序非循环队列：

头文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// ArrayQueue.h
#pragma once

const int MAX_SIZE = 100;
class ArrayQueue 
{
public:
    ArrayQueue();
    bool isEmpty();
    bool isFull();
    void enqueue(int x);
    int dequeue();
    // 获取队列头部元素的值
    int peek();
private:
    int m_data[MAX_SIZE];
    int m_front; 
    int m_rear; 
};
  • const int MAX_SIZE = 100：整形常量，设置队列的最大容量为100
  • int m_front：类的私有成员，队头指针，指向队头元素
  • int m_rear：类的私有成员，队尾指针，用来描述可存储数据的队尾元素在数组中的位置（数组末尾元素的下一个位置）。

源文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
// ArrayQueue.cpp
#include <iostream>
#include "ArrayQueue.h"
using namespace std;

ArrayQueue::ArrayQueue() : m_front(0), m_rear(0) {}

bool ArrayQueue::isEmpty() 
{
    return m_front == m_rear;
}

bool ArrayQueue::isFull() 
{
    return m_rear == MAX_SIZE;
}

void ArrayQueue::enqueue(int x) 
{
    if (isFull()) 
    {
        cout << "队列已经满了, 数据无法入队列!" << endl;
        return;
    }
    m_data[m_rear++] = x;
}

int ArrayQueue::dequeue() 
{
    if (isEmpty()) 
    {
        cout << "空队列, 无法出队列!" << endl;
        return -1;
    }
    return m_data[m_front++];
}

int ArrayQueue::peek() 
{
    if (isEmpty()) 
    {
        cout << "空队列, 无法获取队头元素值!" << endl;
        return -1;
    }
    return m_data[m_front];
}

int main() 
{
    ArrayQueue queue;
    queue.enqueue(1);
    queue.enqueue(2);
    queue.enqueue(3);
    cout << "Front element: " << queue.peek() << endl;  // 输出: 1
    queue.dequeue();
    cout << "Front element after dequeue: " << queue.peek() << endl;  // 输出: 2
    return 0;
}

如果仔细阅读并分析了上面的示例代码之后就会发现它是有缺陷的：

  • 数组尾部作为队列的队尾，用于数据的添加，添加一个数据，队尾指针后移一次
  • 数组头部作为队列的队头，用于数据的删除，删除一个数据，队头指针后移一次

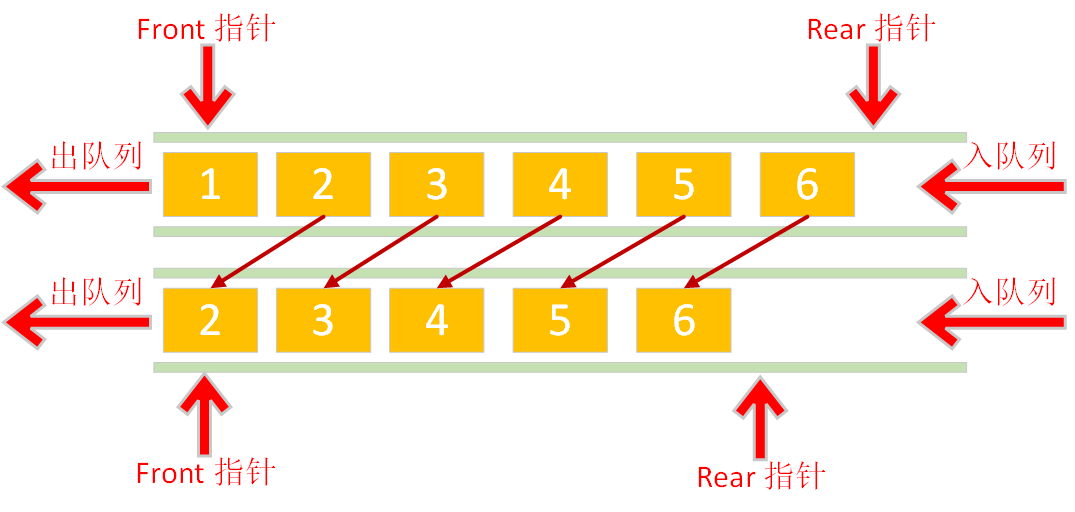
在进行了多次数据的入队和出队之后，队列可能会变成下图的这个样子：

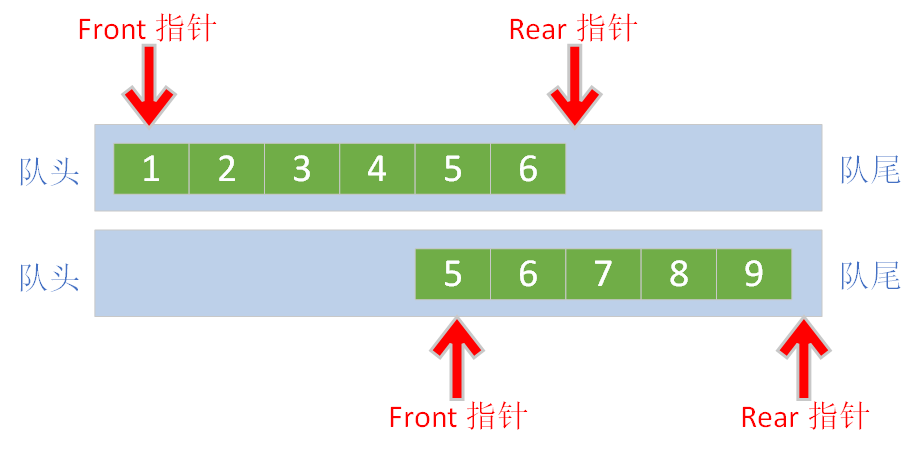
看到这个图我们就会恍然大悟，在上面的代码中虽然让入队列和出队列的时间复杂度都达到了O(1)，与此同时它也使这个队列造成了一种假溢出现象，因为此时的头指针已经不在数组的头部了，而且front 指针之前的存储空间也无法再次被利用。

解决上面的假溢出问题有两种方案：

  1. 让头指针front一直指向数组的起始为止，当出队列的时候，将队列后面的元素依次前移，这样时间复杂度就从O(1)变为了O(n)

  2. 让队列的队尾和队头相接，这样从逻辑上就可以形成一个环状结构，通过这样方式被队头指针跳过的空闲位置，通过队尾指针就可以再次访问到它们并且加以使用了，做了这样的改造之后，插入、删除的时间复杂度还是被维持在了O(1)。

通过分析，很显然第二种解放方案是最优的，那么顺序循环队列该如何使用呢？接下来给大家做详细的讲解。

3. 顺序循环队列

3.1 剖析循环队列

顺序循环队列一般被我们简称为循环队列。它就是在数组的基础上从队列存储空间的最后一个位置绕到第一个位置，形成逻辑上的环状空间，供队列循环使用。

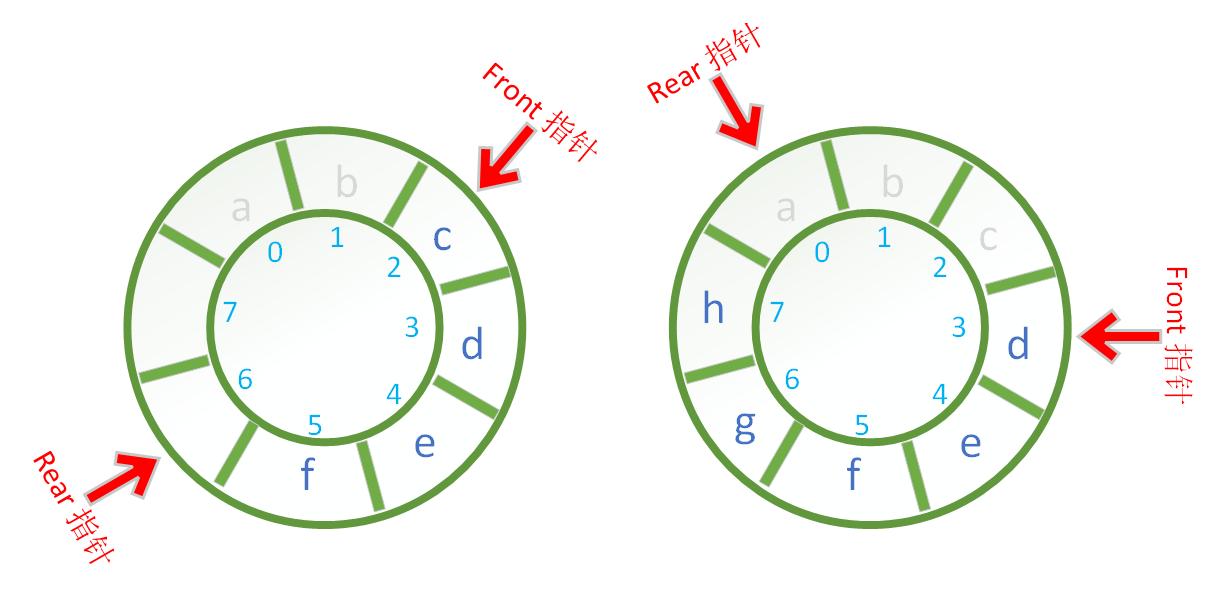
上图中的环形结构的内存在现实中是不存在的，这个环形结构描述的是内存的逻辑结构，对于这个逻辑结构需要说明几点：

  • front指针和rear指针都是顺着顺时针方向转动的
  • 从rear指针位置开始顺时针转动到front指针的前一个位置，这块内存区域都是可用的

循环队列有以下几个特点：

  • 循环队列允许元素在队尾插入，在队头删除，同时遵循先进先出原则
  • 由于循环队列是基于数组实现的，所以它的访问速度很快
  • 如果需要大量添加和删除元素，循环队列比链表更有效率，因为它不需要频繁地移动指针来访问元素。
  • 不支持随机访问元素，因此不能像数组那样直接访问特定位置的元素。

如果想要全面掌握循环队列的使用，我们需要再研究一下循环队列中的一些细节问题：

  1. 如何判断循环队列已经满了？

    当循环队列的rear指针加1之后对队列的总容量capacity取模结果等于front指针，这时表明队列已满，反之则未满。

    (rear + 1) % capacity == front

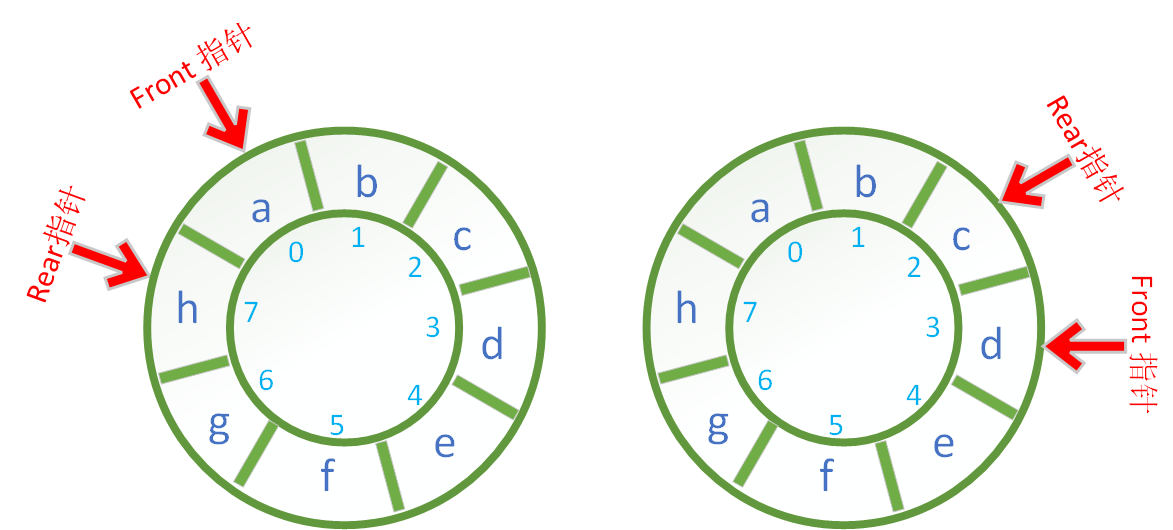
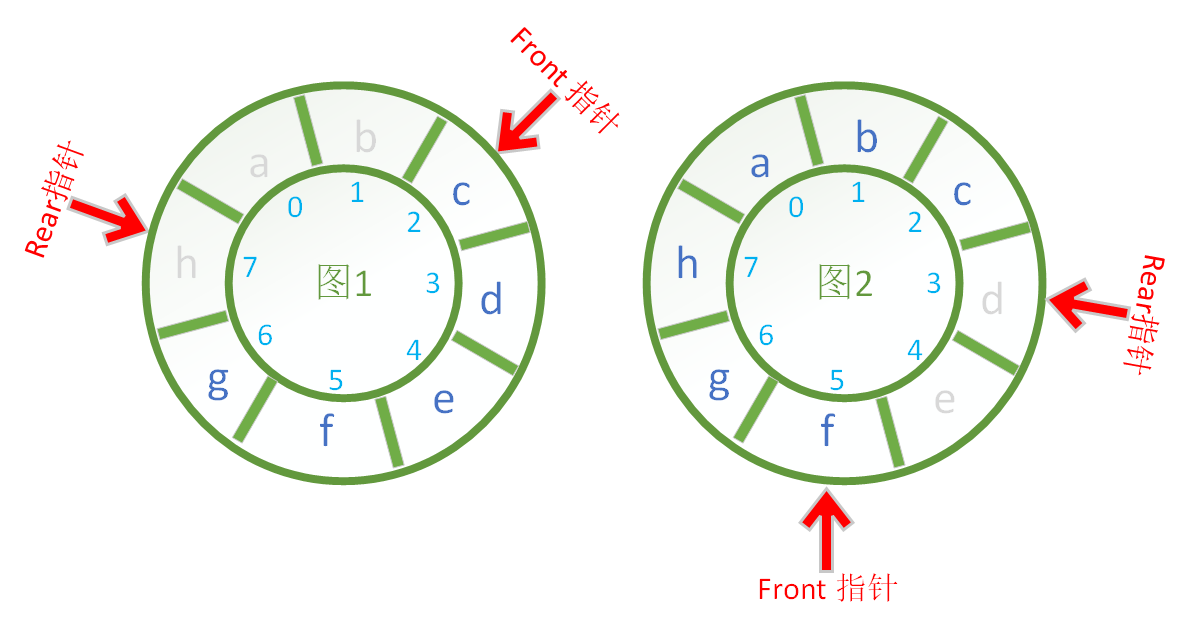
    下面的两幅图都可以表示循环队列已经满了。

  2. 如何判断循环队列为空？

    当循环队列队头指针和队尾指针相等时，说明队列中没有元素，反之则存在元素。

    front == rear

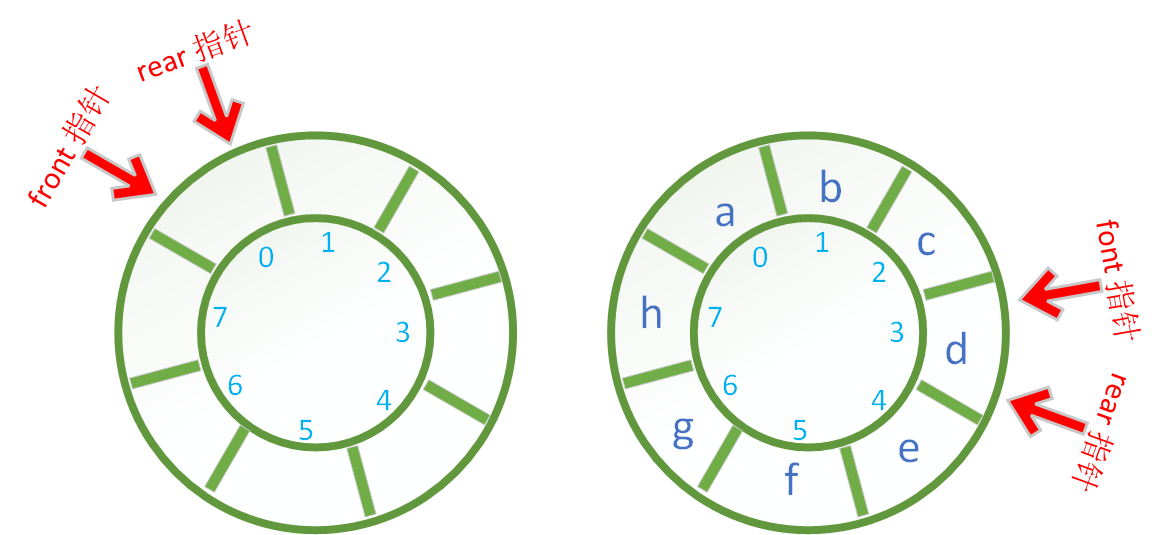
    下面的两幅图都可以表示循环队列是空的。

  3. 由于循环队列是首尾相接的，那么如何确定后移之后的头指针或者尾指针的位置呢？

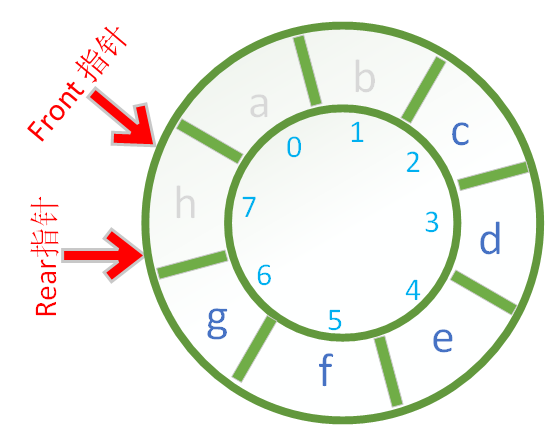
    环形队列的本质是数组，当头指针或者尾指针移动到数组的尾部元素的时候（见下图），如果继续后移就需要让它们指向数组的第一个元素，对应的计算公式如下：

    • 下一个头指针的位置：front = (front + 1) % capacity

    • 下一个尾指针的位置：rear = (rear + 1) % capacity

    其实以上是一个通用公式，头尾指针在任意位置后移之后的新位置都可以通过这种方式来获取。

    image-20240629214912393

  4. 如何确定当前循环队列中的存储的节点数量？

    求循环队列的长度可以通过计算队列的尾指针（rear）和头指针（front）之间的差值，加上最大容量(capacity)，然后对最大容量取模，得到队列的实际长度。

    int size = (rear - front + capacity) % capacity;

    • rear-front：初步计算队尾与队头之间的差值。
    • +capacity：由于是循环队列，可能会产生负值，因此加上 capacity，避免出现负数。
    • %capacity：确保结果在 0 到 capacity-1 之间，这样可以正确表示队列中的元素数量。

    大家可以通过上面提供的公式进行计算，并且在上图中数一下看得到的结果是否相同。

    • 图1 对应的循环队列中存储的元素数量为5个
    • 图2 对应的循环队列中存储的元素数量为6个

3.2 实现一个循环队列

头文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// CircularQueue.h
#pragma once
class CircularQueue 
{
public:
    CircularQueue(int capacity);
    ~CircularQueue();
    bool isEmpty();
    bool isFull();
    void enqueue(int x);
    int dequeue();
    // 获取队头元素的值
    int peek();
private:
    int *m_data;
    int m_front;
    int m_rear;
    int m_size;
    int m_capacity;
};

在上面定义的类中有几个成员变量，简单的介绍一下它们：

  • int m_front：队头指针，指向队头元素
  • int m_rear：队尾指针，指向队尾元素的下一个位置
  • int m_size：队列中存储的实际元素数量
  • int m_capacity：队列的容量

源文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
// CircularQueue.cpp
#include <iostream>
#include "CircularQueue.h"
using namespace std;

CircularQueue::CircularQueue(int capacity) : 
    m_front(0), m_rear(0), m_size(0), m_capacity(capacity), m_data(new int[capacity]) {}

CircularQueue::~CircularQueue()
{
    delete[]m_data;
}

bool CircularQueue::isEmpty() 
{
    return m_size == 0;
}

bool CircularQueue::isFull() 
{
    return m_size == m_capacity;
}

void CircularQueue::enqueue(int x) 
{
    if (isFull()) 
    {
        cout << "队列已经满了, 数据无法入队列!" << endl;
        return;
    }
    m_data[m_rear] = x;
    m_rear = (m_rear + 1) % m_capacity;
    m_size++;
}

int CircularQueue::dequeue() 
{
    if (isEmpty()) 
    {
        cout << "空队列, 无法出队列!" << endl;
        return -1;
    }
    int value = m_data[m_front];
    m_front = (m_front + 1) % m_capacity;
    m_size--;
    return value;
}

int CircularQueue::peek() 
{
    if (isEmpty()) 
    {
        cout << "空队列, 无法获取队头元素值!" << endl;
        return -1;
    }
    return m_data[m_front];
}

int main() 
{
    CircularQueue queue(12);
    queue.enqueue(1);
    queue.enqueue(2);
    queue.enqueue(3);
    cout << "Front element: " << queue.peek() << endl;  // 输出: 1
    queue.dequeue();
    cout << "Front element after dequeue: " << queue.peek() << endl;  // 输出: 2

    return 0;
}

4. 链式队列

链式队列的本质和链式栈一样，都是链表，根据队列的特性选择最简单的单向链表就能满足所有的需求了。接下来我们定义一个C++类把它实现出来。

头文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// LinkedQueue.h
#pragma once

struct Node 
{
    int data;
    Node* next;
    Node(int d) : data(d), next(nullptr) {}
};

class LinkedQueue 
{
public:
    LinkedQueue();
    ~LinkedQueue();
    bool isEmpty();
    void enqueue(int x);
    int dequeue();
    int peek();
private:
    Node* m_front;
    Node* m_rear;   // 队尾指针，指向链表的尾部
};
  • Node* m_front：类的私有成员，队头指针，指向链表的头部
  • Node* m_rear：类的私有成员，队尾指针，指向链表的尾部

源文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
// LinkedQueue.cpp
#include <iostream>
#include "LinkedQueue.h"
using namespace std;

LinkedQueue::LinkedQueue() : m_front(nullptr), m_rear(nullptr) {}

LinkedQueue::~LinkedQueue() 
{
    while (m_front != nullptr) 
    {
        Node* temp = m_front;
        m_front = m_front->next;
        delete temp;
    }
}

bool LinkedQueue::isEmpty() 
{
    return m_front == nullptr;
}

void LinkedQueue::enqueue(int x) 
{
    Node* newNode = new Node(x);
    if (m_rear == nullptr) 
    {
        m_front = m_rear = newNode;
    }
    else 
    {
        m_rear->next = newNode;
        m_rear = newNode;
    }
}

int LinkedQueue::dequeue() 
{
    if (isEmpty()) 
    {
        cout << "空队列, 无法出队列!" << endl;
        return -1;
    }
    Node* temp = m_front;
    int value = temp->data;
    m_front = m_front->next;
    if (m_front == nullptr) 
    {
        m_rear = nullptr;
    }
    delete temp;
    return value;
}

int LinkedQueue::peek() 
{
    if (isEmpty()) 
    {
        cout << "空队列, 无法获取队头元素值!" << endl;
        return -1;
    }
    return m_front->data;
}

int main() 
{
    LinkedQueue queue;
    queue.enqueue(1);
    queue.enqueue(2);
    queue.enqueue(3);
    cout << "Front element: " << queue.peek() << endl;  // 输出: 1
    queue.dequeue();
    cout << "Front element after dequeue: " << queue.peek() << endl;  // 输出: 2

    return 0;
}

通过阅读上面的示例代码可知，实现链式队列使用的是一个不带头结点的单向链表。由于队列是受限制是线性表，只能对链表头部和尾部进行操作，此时使用不带头结点的链表更简单。

既然顺序队列可以也有顺序非循环和顺序循环两种形式，那么大家可以思考这样一个问题：基于链式队列的循环队列和非循环队列，二者是没区别呢，没区别呢，还是没区别呢？

5. 三种队列的总结

队列作为一种基本的数据结构，无论是顺序队列、循环队列还是链式队列，都有其适用的场景和优缺点。顺序队列适合空间需求已知且固定的情况，循环队列适合需要循环利用空间的情况，而链式队列则更适合动态增长和不确定大小的情况。

  • 顺序队列：
    • 优点：实现简单，访问速度快。
    • 缺点：需要预先分配固定大小的空间，可能造成浪费或溢出。
  • 循环队列：
    • 优点：解决了顺序队列的假溢出问题，更高效地利用空间。
    • 缺点：实现相对复杂，操作需要模运算。
  • 链式队列：
    • 优点：没有固定大小限制，可以动态扩展。
    • 缺点：实现复杂，额外的内存开销。

掌握了它们各自的特点之后，使用的时候我们在合适的场景选择合适的模型就OK了。