KMP模式匹配算法

KMP 算法，全称 Knuth-Morris-Pratt 算法，根据三个作者 Donald Knuth、Vaughan Pratt、James H. Morris 的姓氏的首字母拼接而成的。通过这种模式匹配算法可以大大避免字符串在匹配过程中被重复遍历的情况，它将匹配的时间复杂度提升到了 O(m+n)

1. 使用 PMT 表

部分匹配表（Partial Match Table，简称PMT），它记录了模式串的前缀和后缀的最长相等长度，用于在匹配失败时跳过已经匹配的部分，避免回溯，也就是通过已掌握的信息来规避重复的运算。

  • "前缀"：除了最后一个字符外，字符串的所有头部子串
  • "后缀"：除了第一个字符外，字符串的所有尾部子串

以上图的"ABCDABD"为例：

  • “A”的前缀和后缀都为空集，共有元素的长度为0；
  • “AB”的前缀为[A]，后缀为[B]，共有元素的长度为0；
  • “ABC”的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度为0；
  • “ABCD” ，共有元素的长度为0；
    • 前缀为[A, AB, ABC]
    • 后缀为[BCD, CD, D]
  • “ABCDA”，共有元素为”A”，长度为1；
    • 前缀为[A, AB, ABC, ABCD]
    • 后缀为[BCDA, CDA, DA, A]
  • “ABCDAB”，共有元素为”AB”，长度为2；
    • 前缀为[A, AB, ABC, ABCD, ABCDA]
    • 后缀为[BCDAB, CDAB, DAB, AB, B]
  • “ABCDABD”，共有元素的长度为0。
    • 前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]
    • 后缀为[BCDABD, CDABD, DABD, ABD, BD, D]

上图中的部分匹配值就是PMT表中的值，可以直观的看到每个字符在该表中都有一个与之对应的值：

  • 0：表示匹配过程中可以跳过匹配的字符个数为0
  • 1：表示匹配过程中可以跳过匹配的字符个数为1
  • 2：表示匹配过程中可以跳过匹配的字符个数为2

掌握了如何推导PMT表中的值之后，我们来看一下在编程的时候如何实现。

1.1 构建PMT表

PMT表中存储的是一个模式字符串自身的前缀和后缀之间的最长匹配长度，具体来说，PMT 表的每个元素 pmt[i]表示模式串的前 i个字符中，最长的前缀（也即是模式串的起始子串）和后缀（即结束子串）相等的部分的长度。

先来说一下构建PMT表的步骤：

  1. 初始化：
    • 创建一个长度为模式串长度的数组pmt，用来存储部分匹配值。
    • 设定第一个元素pmt[0]为0，因为长度为1的串没有真正的前缀和后缀。
  2. 遍历模式串，定义两个辅助指针i和j：
    • i表示当前字符的位置，j表示当前匹配的前缀长度
    • 设置初始值：i为1，j为0。
  3. 构建过程：
    • 如果模式串的第i个字符与第j个字符相同，说明当前字符匹配成功，则pmt[i] = j + 1，并将i和j分别加1。
    • 如果不匹配，且j不为0，说明当前匹配失败，则将j回溯至pmt[j-1]，继续比较。
    • 如果不匹配，并且j为0，说明无法延续当前的匹配，直接将pmt[i]设为0，并将i加1。

接下来再通过图表的方式为大家描述一下构建PMT表的过程（实线指针表示当前遍历的位置，虚线指针表示移动之后下一次遍历时的位置，没有虚线指针表示不移动）:

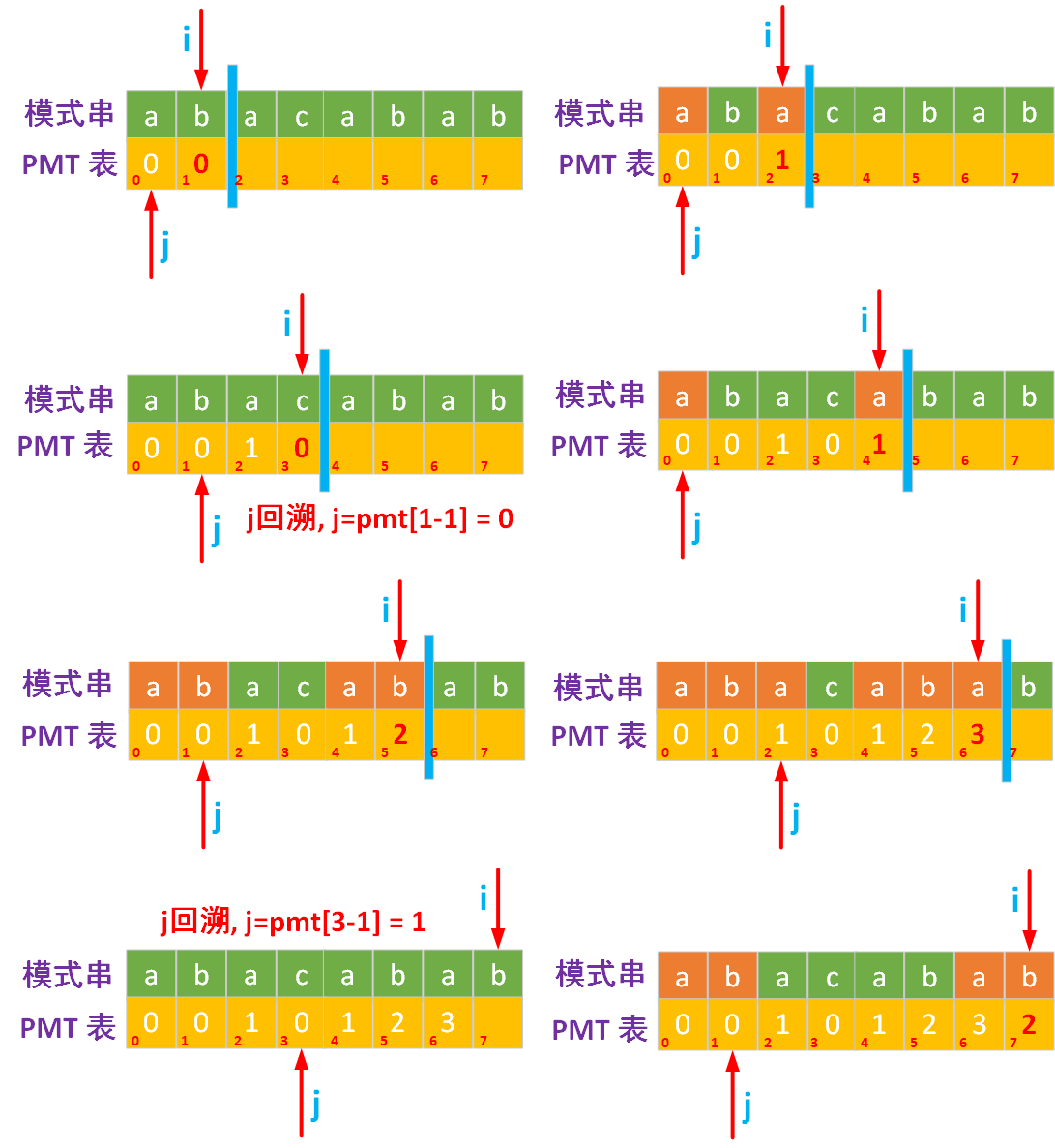
image-20241119184028663

上面的算法中并没有通过循环暴力求解，而是采用了递推的方式，在计算最长前后缀长度过程中有两种情况：

  1. 已知现有前后缀长度，下一个字符依然相同，共同前后缀长度加1，即j++; i++

  2. 已知现有前后缀长度，下一个字符（假设为A）不同，需要做以下处理：

    • 从不包含当前字符的最长前缀中找到它的最长前缀之后的字符，也就是pmt[j-1]位置的字符

      image-20241119231514490

      • 字符c和字符b不等，在此之前的最长前后缀为abc

      • 对于最长前缀abc而言，它的最长前缀为a，它后面的字符为b也就是pmt[1]

      • j需要回溯到pmt[1]的位置，对应的公式为：j = pmt[j-1]

        image-20241119233242080

    • 比较pmt[i]和pmt[j]的值

      • 相等：最长前后缀长度加1，即j++; i++
      • 不相等：重复当前步骤（当 j > 0 时）

这种方式的巧妙之处就是不断利用已掌握的信息来避免重复的运算。

以下是使用C++实现构建PMT表的具体步骤：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
#include <vector>
#include <string>
using namespace std;

vector<int> buildPMT(const string& pattern) 
{
    int m = pattern.length();
    vector<int> pmt(m, 0);
    int j = 0;  

    for (int i = 1; i < m; i++) 
    {
        while (j > 0 && pattern[i] != pattern[j]) 
        {
            j = pmt[j - 1];
        }
        if (pattern[i] == pattern[j]) 
        {
            j++;
        }
        pmt[i] = j;
    }

    return pmt;
}

int main() 
{
    string pattern = "ababaca";
    vector<int> pmt = buildPMT(pattern);

    cout << "PMT表: ";
    for (int i : pmt) 
    {
        cout << i << " ";
    }
    cout << endl;
    return 0;
}

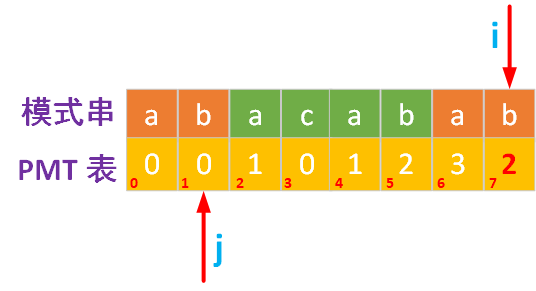
在上面的示例程序中模式串是ababaca：

  • i = 1， j = 0， 比较b和a，不匹配，pmt[1] = 0
  • i = 2， j = 0， 比较a和a，匹配，j++，pmt[2] = 1
  • i = 3，j = 1， 比较b和b，匹配，j++，pmt[3] = 2
  • i = 4， j = 2， 比较a和a，匹配，j++，pmt[4] = 3
  • i = 5， j = 3，比较c和b，不匹配，j = pmt[2] = 1，继续比较c和b，不匹配，j = pmt[0] = 0，pmt[5] = 0
  • i = 6， j = 0， 比较a和a，匹配，j++，pmt[6] = 1

最终得到的PMT表为[0, 0, 1, 2, 3, 0, 1]。

1.2 使用 PMT 表进行模式匹配

在构建好PMT表后，KMP算法就可以通过这个表来进行高效的模式匹配。算法在文本中搜索模式串时，通过PMT表可以在匹配失败时直接跳过已经匹配的部分，从而避免重复比较。

KMP算法基于PMT表的详细模式匹配步骤如下：

  1. 初始化：
    • 设定两个指针i和j，分别指向文本串和模式串的当前字符位置。
    • 初始时i和j都设为0。
  2. 遍历文本串：
    • 使用指针i遍历文本串，同时用指针j遍历模式串。
  3. 匹配过程：
    • 如果文本串的第i个字符与模式串的第j个字符相同，说明当前字符匹配成功，则将i和j分别加1。
    • 如果不相同，且j不为0，说明当前匹配失败，则将j回溯至pmt[j-1]，继续比较。
    • 如果j为0且不匹配，说明无法延续当前的匹配，直接将i加1。
  4. 完成匹配：
    • 当j达到模式串的长度时，说明模式串完全匹配，记录匹配的位置，然后将j回溯至pmt[j-1]继续匹配。

接下来再通过图表的方式为大家演示一下使用KMP算法通过PMT表进行模式匹配的过程（虚线箭头为移动之后的位置）:

image-20241120184408392

最后再为大家阐述一下模式串回溯的核心思想：

  • 在匹配过程中，对文本串的遍历是线性的，一直向后永远不会回退

  • 由于模式串和文本串可能已经匹配了若干字符，当下一个字符不匹配时，回去看最后一个匹配成功的字符（即 j-1 位置）在PMT表中对应的数值，该值表示可以跳过的匹配字符数量。

    在上图中模式串中跳过的两个字符ab和文本串中对应位置的字符是可以完美匹配的。这是因为在匹配失败之前文本串和模式串中都有已经匹配成功的子字符串abcd。

    左图到右图的变化，其本质就是让模式串中abcd的前缀去匹配文本串中abcd的后缀，这无论如何都是可以匹配上的，因此在下一轮比较（右图）的时候可以直接跳过模式串中的这两个字符。

以下是使用C++基于以上的步骤说明写出的实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <iostream>
#include <vector>
#include <string>
using namespace std;

vector<int> buildPMT(const string& pattern) 
{
    int m = pattern.length();
    vector<int> pmt(m, 0);
    int j = 0;
    for (int i = 1; i < m; i++) 
    {
        while (j > 0 && pattern[i] != pattern[j]) 
        {
            j = pmt[j - 1];
        }
        if (pattern[i] == pattern[j]) 
        {
            j++;
        }
        pmt[i] = j;
    }

    return pmt;
}

vector<int> KMP(const string& text, const string& pattern) {
    vector<int> pmt = buildPMT(pattern);
    vector<int> result;
    int n = text.length();
    int m = pattern.length();
    int i = 0; 
    int j = 0; 

    while (i < n) 
    {
        if (text[i] == pattern[j]) 
        {
            i++;
            j++;
        }
        else 
        {
            if (j != 0) 
            {
                j = pmt[j - 1];
            }
            else 
            {
                i++;
            }
        }

        if (j == m) 
        {
            result.push_back(i - j);
            j = pmt[j - 1]; 
        }
    }

    return result;
}

int main() 
{
    string text = "ababcabcabababd";
    string pattern = "ababd";
    vector<int> matches = KMP(text, pattern);

    std::cout << "匹配位置: ";
    for (int pos : matches) 
    {
        cout << pos << " ";
    }
    cout << endl;

    return 0;
}

上面示例程序中的文本串是ababcabcabababd，模式串是ababd：

  • i = 0，j = 0， 比较a和a，匹配，i++，j++
  • i = 1，j = 1， 比较b和b，匹配，i++，j++
  • i = 2， j = 2， 比较a和a，匹配，i++，j++
  • i = 3， j = 3， 比较b和b，匹配，i++，j++
  • i = 4， j = 4， 比较c和d，不匹配，回溯，j = pmt[3] = 2
  • i=4， j=2， 比较 c 和 a， 不匹配，回溯，j = pmt[2-1] = 0
  • i=4，j=0，比较 c 和 a，无法回溯，i = 5
  • i=5，j=0，比较 a 和 a，匹配，i++，j++
  • 继续匹配直到找到完全匹配的位置或遍历完文本串。

通过上述过程，KMP算法能够在O(n + m)的时间复杂度内完成模式匹配，极大地提高了匹配效率。

2. 使用 next 数组

Next数组的作用是记录模式串中各位置的前缀和后缀的最长匹配长度，用于在匹配过程中遇到不匹配时，

模式串应该回溯的位置。与PMT表的核心思想一致，但是记录方式有些许差异：

  • PMT 表中的 pmt[i] 表示包括当前字符在内的最长前后缀长度（即可以跳过匹配的字符数量）
  • Next 表中的 next[i] 表示当前字符之前（不包含当前字符）的最长前后缀长度（即可以跳过匹配的字符数量）
    • 特殊情况：next[0] = -1，因为单一字符不满足公共前后缀的概念设定。

2.1 构建 next 数组

如果想要基于模式串构建 next 数组，其具体步骤如下：

  1. 初始化阶段：

    • 创建长度为模式串长度的 next 数组
    • 设置 next[0] = -1（固定值）
    • 初始化两个指针：i = 0（后缀末尾），j = -1（前缀末尾）

  2. 主要计算过程：

    • 从左到右遍历模式串，计算每个位置的 next 值
    • 对于位置 i，比较 pattern[i] 和 pattern[j]：
      • 如果相等：i 和 j 都右移，next[i+1] = j+1
      • 如果不等：j 回退到 next[j]，继续比较（回退机制，见步骤3）
      • 如果 j 回退到 -1：i 右移，j 变为 0，next[i] = 0

  3. 回退机制：

    • 当字符不匹配时，j 指针通过查找 next[j] 快速回退
    • 回退过程可能会连续多次，直到找到匹配或回退到 -1

  4. 终止条件：

    • 当 i 遍历完整个模式串（除最后一个字符）时结束，此时 next 数组构建完成

这个过程本质上是在寻找每个位置的最长相等前后缀，通过已经计算好的 next 值来加速计算过程。

接下来再通过图表的方式为大家描述一下构建next数组的过程（虚线指针表示移动之后的位置，没有虚线指针表示不移动）:

image-20241121103606278
  • 第一步：由于 j = -1，执行i++，j++，next[1] = j = 0
  • 第二步：i = 1，j = 0
    • 比较 pattern[1] 和 pattern[0]：’a’ = ‘a’
    • 匹配成功，执行 i++，j++，next[2] = j = 1
image-20241121104406235

第三步：i = 2，j = 1

  • 比较 pattern[2] 和 pattern[1]：’b’ != ‘a’
  • 不匹配，j 回退：j = next[j] = next[1] = 0
  • 再比较 pattern[2] 和 pattern[0]：’b’ != ‘a’
  • 不匹配，j 回退：j = next[j] = next[0] = -1
  • j = -1，执行i++，j++，next[3] = j = 0
image-20241121104808271
  • 步骤4：i = 3，j = 0
    • 比较 pattern[3] 和 pattern[0]：’a’ = ‘a’
    • 匹配成功，执行 i++，j++，next[4] = j = 1
  • 步骤5： i = 4，j = 1
    • 比较 pattern[4] 和 pattern[1]：’a’ = ‘a’
    • 匹配成功，执行 i++，j++，next[5] = j = 2
image-20241121105128320

步骤6：i = 5，j = 2

  • 比较 pattern[5] 和 pattern[2]：’a’ != ‘b’
  • 不匹配，j回退：j = next[j] = next[2] = 1
  • 比较 pattern[5] 和 pattern[1]：’a’ = ‘a’
  • 匹配成功，执行 i++，j++，next[6] = j = 2

以下是使用C++实现构建Next数组的具体步骤：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <iostream>
#include <vector>
#include <string>
using namespace std;

vector<int> buildNext(const string& pattern)
{
    int len = pattern.size();
    vector<int> next(len, -1);
    int j = -1, i = 0;

    while (i < len - 1)
    {
        if (j == -1 || pattern[i] == pattern[j])
        {
            i++;
            j++;
            next[i] = j;
        }
        else
        {
            j = next[j];	// 回溯
        }
    }

    return next;
}

int main() 
{
    string pattern = "ababaca";
    vector<int> next = buildNext(pattern);

    cout << "Next数组: ";
    for (int i : next) 
    {
        cout << i << " ";
    }
    cout << endl;

    return 0;
}

为了便于大家理解，下面再次复盘一下上面程序中 next 数组的构建过程：

模式串：a b a b a c a
下 标：0 1 2 3 4 5 6

  1. 初始化：

    • next[0] = -1（固定值）

    • i = 0（后缀指针）

    • j = -1（前缀指针）

  2. 逐步计算：

    • 第一步：计算 next[1]，i=0，j=-1

      • 由于j=-1，执行i++，j++，next[1] = j = 0

    • 第二步：计算 next[2]，i=1，j=0

      • 比较 pattern[1] 和 pattern[0]：’b’ ≠ ‘a’
      • j 回退到 next[0]=-1
      • 由于j=-1，执行i++，j++，next[2] = j = 0

    • 第三步：计算 next[3]，i=2，j=0

      • 比较 pattern[2] 和 pattern[0]：’a’ = ‘a’
      • 匹配成功，执行i++，j++，next[3] = j = 1

    • 第四步：计算 next[4]，i=3，j=1

      • 比较 pattern[3 ]和 pattern[1]：’b’ = ‘b’
      • 匹配成功，执行i++，j++，next[4] = j = 2

    • 第五步：计算 next[5]，i=4，j=2

      • 比较pattern[4]和pattern[2]：’a’ = ‘a’
      • 匹配成功，执行i++，j++，next[5] = j = 3

    • 第六步：计算next[6]，i=5，j=3

      • 比较 pattern[5] 和 pattern[3]：’c’ ≠ ‘b’
      • j 回退到next[3]=1
      • 比较 pattern[5] 和 pattern[1]：’c’≠’b’
      • j 回退到 next[1] = 0
      • 比较 pattern[5] 和 pattern[0]：’c’≠’a’
      • j 回退到 next[0]=-1
      • 由于 j=-1，执行 i++，j++，next[6] = j = 0

最终next数组：[-1, 0, 0, 1, 2, 3, 0]

通过构建Next数组，KMP算法能够高效地进行字符串匹配，在匹配失败时利用已知的部分匹配信息，避免重复比较，提高了算法效率。

2.2 使用 next 数组进行模式匹配

KMP算法在匹配过程中除了使用PMT表还可以使用Next数组，当遇到不匹配时，可以根据Next数组的信息跳过一些不必要的匹配，从而提高效率。

使用 next 数组进行 KMP 模式匹配的核心步骤如下：

  1. 初始化阶段：

    • 预先计算模式串的 next 数组，并定义两个辅助指针 i 和 j
    • 初始化主串指针 i = 0，初始化模式串指针 j = 0

  2. 匹配过程 – 循环比较主串和模式串字符，直到以下任一条件满足：

    • 主串遍历完（i 到达末尾）
    • 模式串遍历完（找到匹配）
    • 发生失配需要移动模式串

  3. 处理规则：

    • 当字符匹配时（text[i] == pattern[j]）：

      • i 和 j 都向右移动
      • 如果 j 达到模式串长度，说明找到一个匹配

    • 当字符不匹配时（text[i] != pattern[j]）：

      • j 回退到 next[j] 的位置，i 保持不变

      • 如果 j 变为 -1，则 i 和 j 都右移

  4. 关键特点：

    • 主串指针 i 永远不会回退
    • 模式串指针 j 通过 next 数组实现快速移动
    • 找到匹配后，可以继续寻找下一个匹配位置

接下来再通过图表的方式为大家演示一下使用KMP算法通过next数组（从0号位开始）进行模式匹配的过程:

  1. i=4， j=4： ‘c’ ≠ ‘a’ 匹配失败！

  2. j 回退到 next[4] = 2

  1. i=4，j=2：’c’ ≠ ‘a’，匹配失败！

    • j 回退到 next[2] = 0

  2. i=4，j=0：’c’ ≠ ‘a’，匹配失败！

    • j 回退到 next[0] = -1

  3. j == -1，i++，j++

  1. i=7，j=2：’c’ ≠ ‘a’，匹配失败！

    • j 回退到 next[2] = 0

  2. i=7，j=0：’c’ ≠ ‘a’，匹配失败！

    • j 回退到 next[0] = -1

  3. j == -1，i++，j++

  1. 当模式串和文本串匹配成功之后，i=14，j = 6，数组越界，需要让 j 指向 next 数组最后一个元素，即 j = j-1 = 5

  2. i=14，j=5：’d’ ≠ ‘b’，匹配失败！

    • j 回退到 next[5] = 3

  3. i=14，j=3：’d’ ≠ ‘b’，匹配失败！

    • j 回退到 next[3] = 1

  4. i=14，j=1：’d’≠’b’ ，匹配失败！

    • j 回退到 next[1] = 0

  5. i=14，j=0：’d’ ≠ ‘a’ ，匹配失败！

    • j 回退到 next[0] = -1

根据也以上描述，我们就可以把对应的C++代码写出来了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <iostream>
#include <vector>
#include <string>
using namespace std;

// 计算next数组
vector<int> getNext(const string& pattern) 
{
    int n = pattern.length();
    vector<int> next(n);
    next[0] = -1;
    int j = -1;
    int i = 0;
    
    while (i < n - 1) 
    {
        if (j == -1 || pattern[i] == pattern[j]) 
        {
            i++;
            j++;
            next[i] = j;
        } 
        else 
        {
            j = next[j];
        }
    }
    return next;
}

// KMP搜索，返回所有匹配位置
vector<int> kmpSearch(const string& text, const string& pattern) 
{
    vector<int> positions;  // 存储所有匹配位置
    if (pattern.empty()) return positions;
    
    vector<int> next = getNext(pattern);
    int i = 0;  // 主串指针
    int j = 0;  // 模式串指针
    
    while (i < text.length()) 
    {
        if (j == -1 || text[i] == pattern[j]) 
        {
            i++;
            j++;
            if (j == pattern.length()) // 找到一个匹配
            {  
                positions.push_back(i - j);  // 记录匹配位置
                cout << "找到匹配, i = " << i << ", j = " << j << endl;
                j = next[j - 1];  // 继续寻找下一个匹配
            }
        } 
        else 
        {
            j = next[j];  // 失配时，模式串指针回退
        }
    }
    return positions;
}

int main() 
{
    string text = "ababcabcabababdabababxyz";
    string pattern = "ababab";
    
    // 查找所有匹配位置
    vector<int> matches = kmpSearch(text, pattern);
    
    // 打印结果
    if (matches.empty()) 
    {
        cout << "未找到匹配" << endl;
    } 
    else 
    {
        cout << "找到匹配位置: ";
        for (int pos : matches) 
        {
            cout << pos << " ";
        }
        cout << endl;
        
        // 打印每个匹配的具体情况
        for (int pos : matches) 
        {
            cout << "位置 " << pos << ": ";
            cout << text.substr(pos, pattern.length()) << endl;
        }
    }
    
    return 0;
}

程序输出的结果为：

1
2
3
4
5
6
Next数组: -1 0 0 1 2 3
找到匹配, i = 14, j = 6
找到匹配, i = 21, j = 6
找到匹配位置: 8 15
位置 8: ababab
位置 15: ababab

关于匹配的过程在上面的图例中已经做了非常详细的讲解，此处就不在过多赘述。关键点说明：

  1. 主串指针 i 始终向前移动，不会回退

  2. 模式串指针 j 在失配时通过 next 数组回退

  3. 每次失配都利用 next 数组跳过不必要的比较

在本例中找到了两次完整匹配，这个例子很好地展示了：连续匹配时的前进过程、失配时的多次回退以及 next 数组在加速匹配中的作用。

3. 使用 nextval 数组

3.1 next 数组的缺陷和优化

在上面使用 next 数组进行 KMP 模式匹配的例子中，有这样的一个细节，如下图：

  1. i=4， j=4： ‘c’ ≠ ‘a’ 匹配失败！

    • j 回退到 next[4] = 2

  2. i=4，j=2：’c’ ≠ ‘a’，匹配失败！

    • j 回退到 next[2] = 0

  3. i=4，j=0：’c’ ≠ ‘a’，匹配失败！

    • j 回退到 next[0] = -1

  4. j == -1，i++，j++

对于第 1，2，3 个步骤而言，回溯之前 j 位置的字符值为a，连续回溯了两次之后 j 位置的字符值依旧为a，当再次回溯时 next[j] 的值为 -1 ，停止继续回溯。

对于上面的回溯过程其实是可以优化的，如果想要一步到位就需要让 next[4] = next[2] = next[0] = -1，也就是在公共前后缀中如果发现了相同的字符，需要让当前字符（位置记作 i）的 next 元素值等于上一个字符（位置记作j）的 next 元素值，即：next[i] = next[j]。

当在文本串中找到了一个完整的模式串匹配之后，继续向后匹配搜索下一个，具体步骤如下：

  1. 当模式串和文本串匹配成功之后，i=14，j = 6，数组越界，需要让 j 指向 next 数组最后一个元素，即 j = j-1 = 5

  2. i=14，j=5：’d’ ≠ ‘b’，匹配失败！

    • j 回退到 next[5] = 3

  3. i=14，j=3：’d’ ≠ ‘b’，匹配失败！

    • j 回退到 next[3] = 1

  4. i=14，j=1：’d’≠’b’ ，匹配失败！

    • j 回退到 next[1] = 0

  5. i=14，j=0：’d’ ≠ ‘a’ ，匹配失败！

    • j 回退到 next[0] = -1，匹配结束。

对于第 2，3，4 个步骤而言，回溯之前 j 位置的字符值为b，连续回溯了两次之后 j 位置的字符值依旧为b，当再次回溯时模式串中 j 位置的字符值为 a 不等于 b ，停止继续回溯。

对于上面的回溯过程同样可以优化，如果想要一步到位就需要让 next[5] = next[3] = next[1] = 0，也就是在公共前后缀中如果发现了相同的字符需要让当前字符（位置记作 i）的 next 元素值等于上一个字符（位置记作j）的 next 元素值，即：next[i] = next[j]。

基于以上分析就可以完成对 next 数组的优化了，一般我们将优化之后的 next 数组称之为 nextval 数组。

下面是关于 nextval 数组的具体构建过程：

  1. 第一轮：j = -1，i = 0
    • 由于 j = -1，所以 i++， j++， next[1] = 0
  2. 第二轮：i = 1， j = 0
    • pattern[i] ！= pattern[j]，即 ‘a’ != ‘b’
    • j 回溯，j = next[0] = -1
  3. 第三轮：i = 1， j = -1
    • 由于 j = -1，所以 i++， j++，i = 2，j = 0
    • i，j 指针后移之后需要再比较一次 pattern[i] == pattern[j]，’a’ == ‘a’，所以 next[2] = -1
      • 相等： next[i] = next[j]
      • 不等：next[i] = j
  1. 第四轮：i = 2，j = 0
    • pattern[i] == pattern[j]，即：’a’ == ‘a’，i++，j++
    • i，j 指针后移之后需要再比较一次 pattern[i] == pattern[j]，’b’ == ‘b’，所以 next[3] = 0
      • 相等： next[i] = next[j]
      • 不等：next[i] = j
  2. 第五轮：i = 3，j = 1
    • pattern[i] == pattern[j]，即：’b’ == ‘b’，i++，j++
    • i，j 指针后移之后需要再比较一次 pattern[i] == pattern[j]，’a’ == ‘a’，所以 next[4] = -1
      • 相等： next[i] = next[j]
      • 不等：next[i] = j
  3. 第六轮：i = 4，j = 2
    • pattern[i] == pattern[j]，即：’a’ == ‘a’，i++，j++
    • i，j 指针后移之后需要再比较一次 pattern[i] == pattern[j]，’b’ == ‘b’，所以 next[5] = 0
      • 相等： next[i] = next[j]
      • 不等：next[i] = j

最后再总结下关于 next 数组和 nextval 数组构建过程的主要区别（当 pattern[i] == pattern[j] 条件成立时）：

  1. next 数组：
    • i++，j++
    • next[i] = j
  2. nextval 数组：
    • i++，j++
    • 再次判断 pattern[i] == pattern[j] 条件是否成立
      • 成立：next[i] = next[j]
      • 不成立：next[i] = j

思路掌握之后，再来说一下代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <vector>
#include <string>
using namespace std;

vector<int> buildNext(const string& pattern)
{
    int size = pattern.size();
    vector<int> next(size, -1);
    int i = 0, j = -1;

    int count = 1;
    while (i < size - 1)
    {
        if (j == -1 || pattern[i] == pattern[j])
        {
            i++;
            j++;
            // 优化 next 数组
            if (pattern[i] == pattern[j])
            {
                next[i] = next[j];
            }
            else
            {
                next[i] = j;
            }
        }
        else
        {
            j = next[j];	// 回溯
        }
        count++;
    }

    return next;
}

int main()
{
    string pattern = "ababab";
    vector<int> next = buildNext(pattern);

    cout << "Next数组: ";
    for (int i : next)
    {
        cout << i << " ";
    }
    cout << endl;

    return 0;
}

3.3 使用 nextval 数组进行模式匹配

使用 nextval 数组进行模式匹配和使用 next 数组进行模式匹配的流程完全相同，区别就是在和某些特定格式的模式串（模式串中有若干重复的子串）就行匹配的时候效率提高了，因为模式串回溯的次数减少了，比较的次数也较少了。

使用 nextval 数组进行模式匹配的代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
#include <iostream>
#include <vector>
#include <string>
using namespace std;

vector<int> getNextval(const string& pattern)
{
    int size = pattern.size();
    vector<int> next(size, -1);
    int i = 0, j = -1;

    int count = 1;
    while (i < size - 1)
    {
        if (j == -1 || pattern[i] == pattern[j])
        {
            i++;
            j++;
            // 优化 next 数组
            if (pattern[i] == pattern[j])
            {
                next[i] = next[j];
            }
            else
            {
                next[i] = j;
            }
        }
        else
        {
            j = next[j];	// 回溯
        }
        count++;
    }

    return next;
}

// KMP搜索，返回所有匹配位置
vector<int> kmpSearch(const string& text, const string& pattern)
{
    vector<int> positions;  // 存储所有匹配位置
    if (pattern.empty()) return positions;

    vector<int> next = getNextval(pattern);
    int i = 0;  // 主串指针
    int j = 0;  // 模式串指针

    while (i < text.length())
    {
        if (j == -1 || text[i] == pattern[j])
        {
            i++;
            j++;
            if (j == pattern.length()) // 找到一个匹配
            {
                positions.push_back(i - j);  // 记录匹配位置
                cout << "找到匹配, i = " << i << ", j = " << j << endl;
                j = next[j - 1];  // 继续寻找下一个匹配
            }
        }
        else
        {
            j = next[j];  // 失配时，模式串指针回退
        }
    }
    return positions;
}

int main()
{
    string text = "ababcabcabababdabababxyz";
    string pattern = "ababab";

    // 查找所有匹配位置
    vector<int> matches = kmpSearch(text, pattern);

    // 打印结果
    if (matches.empty())
    {
        cout << "未找到匹配" << endl;
    }
    else
    {
        cout << "找到匹配位置: ";
        for (int pos : matches)
        {
            cout << pos << " ";
        }
        cout << endl;

        // 打印每个匹配的具体情况
        for (int pos : matches)
        {
            cout << "位置 " << pos << ": ";
            cout << text.substr(pos, pattern.length()) << endl;
        }
    }

    return 0;
}

关于匹配的具体流程，此处就不再进行逐条分析，可以参考本文档的 2.2 章节，一模一样。