1. 二叉树搜索树概述

二叉搜索树（Binary Search Tree, BST）也叫二叉排序树（Binary Sort Tree），是一种特殊的二叉树，它满足以下性质：

1. 左子树：左子树上所有节点的值都小于根节点的值。
2. 右子树：右子树上所有节点的值都大于根节点的值。
3. 递归性质：左子树和右子树本身也是二叉排序树。

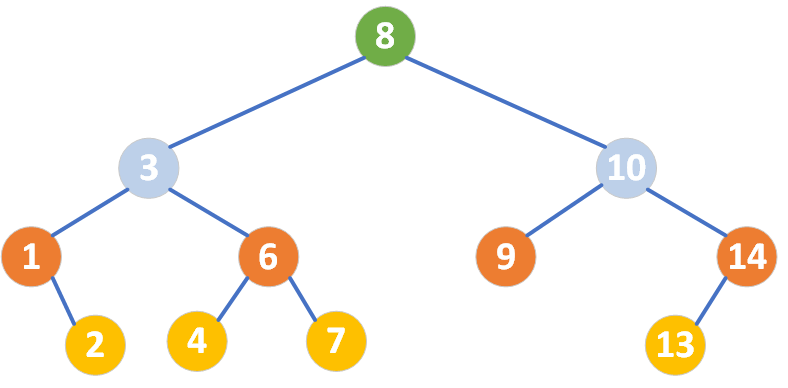
二叉搜索树的一个重要特性是，它的中序遍历（左 → 根 → 右）结果是一个有序的序列。因此，二叉搜索树常用于实现动态集合的查找、插入和删除操作。

2. 二叉搜索树的基本操作

2.1 查找操作

二叉搜索树（BST）的查找操作是一种高效的算法，其平均时间复杂度为 O(log n)。查找步骤是基于二叉搜索树的特性：对于每个节点，左子树的所有节点值小于当前节点，右子树的所有节点值大于当前节点。以下是详细的查找步骤：

1. 从根节点开始：查找操作必须从二叉搜索树的根节点开始。
2. 比较目标值与当前节点值
   • 如果 目标值 == 当前节点值，查找成功，返回该节点。
   • 如果 目标值 < 当前节点值，则递归查找左子树。
   • 如果 目标值 > 当前节点值，则递归查找右子树。
3. 递归或迭代查找：重复上述比较过程，直到找到目标值或到达叶子节点（查找失败）。
4. 查找结束
   • 如果找到目标值，返回对应的节点。
   • 如果到达叶子节点仍未找到目标值，则返回 nullptr 或表示查找失败的值。

以下图的二叉搜索树为例，查找目标 7，具体查找过程如下：

1. 从根节点 8 开始
   • 7 < 8，向左子树查找。
2. 访问节点 3
   • 7 > 3，向右子树查找。
3. 访问节点 6
   • 7 > 6，向右子树查找。
4. 访问节点 7
   • 7 == 7，查找成功，返回节点 7。

2.2 插入操作

二叉搜索树（BST）的插入操作是构建和维护二叉搜索树的关键操作之一。平均情况下，插入操作的时间复杂度为 O(log n)，其中 n 是树中节点的数量。插入操作的核心思想是利用二叉搜索树的性质，将新节点插入到正确的位置，保持树的结构。以下是详细的插入步骤：

1. 从根节点开始：插入操作从二叉搜索树的根节点开始。如果树为空，则新节点成为根节点。
2. 比较新节点的值与当前节点的值
   • 如果 新节点的值 < 当前节点的值，递归向左子树插入。
   • 如果 新节点的值 > 当前节点的值，递归向右子树插入。
   • 如果 新节点的值 == 当前节点的值，根据具体需求决定是否插入（BST 中通常不允许重复值）。
3. 找到插入位置：重复上述比较过程，直到找到一个空位置（即 nullptr），然后将新节点插入到该位置。
4. 插入完成：新节点被插入到树中，树的结构保持不变。

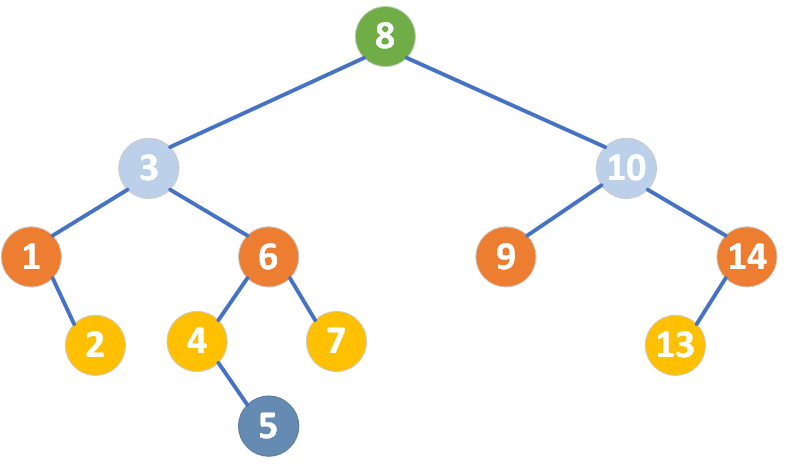
还是以上图的二叉搜索树为例，插入目标值 5，具体插入过程如下：

1. 从根节点 8 开始
   • 5 < 8，向左子树插入。
2. 访问节点 3
   • 5 > 3，向右子树插入。
3. 访问节点 6
   • 5 < 6，向左子树插入。
4. 访问节点 4
   • 5 > 4，向右子树插入。
5. 找到空位置
   • 节点 4 的右子节点为空，将新节点 5 插入到此处。

2.3 删除操作

二叉搜索树（BST）的删除操作是构建和维护二叉搜索树的关键操作之一。平均情况下，删除操作的时间复杂度为 O(log n)，其中 n 是树中节点的数量。删除节点需要保持二叉搜索树的性质（左子树的所有值小于根节点，右子树的所有值大于根节点）。删除操作有以下三种情况：

1. 删除叶子节点：如果待删除节点没有子节点，直接删除即可。
2. 删除只有一个子节点的节点：如果待删除节点只有一个子节点，用其子节点替代被删除的节点。
3. 删除有两个子节点的节点：
   • 找到其右子树的最小值节点（或左子树的最大值节点）
   • 用该节点的值替换待删除节点的值，然后删除该节点。

删除节点的详细步骤如下：

1. 查找待删除节点：从根节点开始，递归或迭代查找待删除节点。

2. 根据情况删除节点

   • 情况 1：待删除节点是叶子节点，直接删除该节点，并将其父节点的对应指针设置为 nullptr。

     例如，删除叶子节点 8，删除前的二叉搜索树如下：

     1 2 3 4 5

     3 / \ 1 6 / \ 4 8

     删除后的二叉搜索树如下：

     1 2 3 4 5

     3 / \ 1 6 / 4

   • 情况 2：待删除节点只有一个子节点，用其子节点替代被删除的节点，并更新父节点的指针。

     例如，删除节点 6（只有一个右子节点），删除前的二叉搜索树如下：

     1 2 3 4 5

     3 / \ 1 6 / 4

     删除后的二叉搜索树如下：

     1 2 3

     3 / \ 1 4

   • 情况 3：待删除节点有两个子节点，找到其右子树的最小值节点（或左子树的最大值节点），用该节点的值替换待删除节点的值，然后删除该节点。

     例如，删除节点 3，删除前的二叉搜索树如下：

     1 2 3 4 5

     3 / \ 1 6 / \ 4 8

     • 找到右子树的最小值节点 4。
     • 将节点 3 的值替换为 4。
     • 删除节点 4。

     删除后的二叉搜索树如下：

     1 2 3 4 5

     4 / \ 1 6 \ 8

3. 二叉搜索树的实现

对于一棵二叉搜索树而言，在它的每个节点中存储的数据可以是基础类型，也可以是复合类型，所以为了增强数据的处理能力，我们可以可以把二叉搜索树类定义成一个泛型类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

// bstree.hpp
template<typename T, typename CompFunc = less<T>>
class BST
{
public:
    struct Node
    {
        Node(T value = T()) : data(value), left(nullptr), right(nullptr) {}
        T data;         // 数据域
        Node* left;     // 左孩子
        Node* right;    // 右孩子
    };
    // 类成员函数
    BST(CompFunc comp = CompFunc());
    ~BST();
    // 非递归
    void insertNormal(const T& value);
    void removeNormal(const T& value);
    Node* queryNormal(const T& value);
    // 递归
    void insert(const T& value);
    void remove(const T& value);
    Node* query(const T& value);
    // 递归中序遍历二叉树
    void inorder();

private:    
    // 内部接口
    // 递归中序遍历二叉树
    void inorder(Node* root);
    Node* insert(Node* root, const T& value);
    Node* remove(Node* root, const T& value);
    Node* query(Node* root, const T& value);
    // 释放树节点
    void clear(Node* root);

private:
    Node* m_root;       // 根节点
    CompFunc m_comp;    // 函数对象(可调用对象)
};

template<typename T, typename CompFunc = less<T>> 是 C++ 中的模板声明语法，用于定义一个通用的类或函数，使其能够处理多种数据类型。

1. template<typename T>
   表示定义一个模板，T 是一个占位符类型，可以在实例化时替换为具体的类型（如 int、double、std::string 等）。

2. typename CompFunc = less<T>
   表示第二个模板参数 CompFunc，默认值为 std::less<T>，即默认使用 std::less 来比较两个 T 类型的值。CompFunc 可以是一个函数对象或函数指针，用于定义自定义的比较逻辑。

std::less<T> 的定义如下：

1
2
3
4
5
6
7
8

template<typename T>
struct less 
{
    bool operator()(const T& lhs, const T& rhs) const 
    {
        return lhs < rhs;
    }
};

• operator()：这是 std::less<T> 的核心函数，用于比较两个值 lhs 和 rhs。
• 返回值：如果 lhs < rhs，返回 true；否则返回 false。

如果想要自定义比较函数，按照上面的std::less<T>示例如法炮制即可, 比如:

1
2
3
4
5
6
7
8

template<typename T>
struct MyComparator 
{
    bool operator()(const T& a, const T& b) const 
    {
        return a > b; // 从大到小排序
    }
};

3.1 构造和析构

C++ 的模板是一种编译时机制，模板代码在编译时根据具体类型生成具体的代码（即模板实例化）。与普通函数或类不同，模板的定义和实现不能分离到 .h 和 .cpp 文件中，原因如下：

普通函数/类的编译模型：

• 声明（.h 文件）：告诉编译器函数或类的存在和接口。
• 定义（.cpp 文件）：提供函数或类的具体实现。
• 编译器在编译 .cpp 文件时生成目标代码，链接器在链接时将声明和定义关联起来。

模板的编译模型：

• 模板的实例化需要在编译时完成，因此编译器必须能够看到模板的完整定义（包括实现）。
• 如果将模板的实现放到 .cpp 文件中，编译器在编译其他使用模板的源文件时无法看到模板的实现，导致无法实例化模板。
• 对于模板代码，编译器的处理流程如下：
  1. 词法分析和语法分析：与非模板代码相同。
  2. 模板解析：解析模板定义，但不生成代码。
  3. 模板实例化：在模板被使用时（如 BST<int>），生成具体的代码。
  4. 代码生成：生成目标机器代码。

为了防止编译器无法看到模板类的完整实现，导致实例化失败，我们通常会将模板的定义和实现都写在同一个 .hpp 文件中。下面是定义的二叉搜索类的构造和析构函数的实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

// bstree.hpp
template<typename T, typename CompFunc>
BST<T, CompFunc>::BST(CompFunc comp) : m_root(nullptr), m_comp(comp) {}

template<typename T, typename CompFunc>
BST<T, CompFunc>::~BST()
{
    clear(m_root);
    m_root = nullptr;
}

template<typename T, typename CompFunc>
void BST<T, CompFunc>::clear(Node* root)
{
    if (root == nullptr)
    {
        return; // 递归结束
    }
    // 释放左子树
    clear(root->left);
    // 释放右子树
    clear(root->right);
    // 释放根节点
    delete root;
}

3.1.1 构造函数

1
2

template<typename T, typename CompFunc>
BST<T, CompFunc>::BST(CompFunc comp) : m_root(nullptr), m_comp(comp) {}

功能：

• 初始化 BST 的根节点 m_root 为 nullptr，表示树为空。
• 初始化比较函数对象 m_comp，用于比较节点值。

参数：

• comp：比较函数对象，默认值为 CompFunc()（即 std::less<T>，用于升序排序）。

示例：

1
2

BST<int> bst;                      // 使用默认比较函数 std::less<int>
BST<int, std::greater<int>> bst2;  // 使用 std::greater<int> 作为比较函数

3.1.2 析构函数

1
2
3
4
5
6

template<typename T, typename CompFunc>
BST<T, CompFunc>::~BST()
{
    clear(m_root);
    m_root = nullptr;
}

功能：

• 调用 clear(m_root) 递归释放树中所有节点的内存。
• 将根节点 m_root 置为 nullptr，避免悬空指针。

实现细节：

• clear(Node* root) 是一个辅助函数，用于递归释放树中所有节点的内存。
• 递归释放过程：
  1. 如果当前节点为空，直接返回。
  2. 递归释放左子树。
  3. 递归释放右子树。
  4. 释放当前节点。

3.2 插入操作

3.2.1 非递归实现

在二叉搜索树种插入新节点，核心逻辑如下：

1. 树为空：
   • 如果根节点 m_root 为空，直接将新节点作为根节点。
2. 搜索插入位置：
   • 使用 cur 指针从根节点开始遍历树。
   • 使用 parent 指针保存 cur 的父节点地址。
   • 如果当前节点的值等于待插入值，提示插入失败并返回。
   • 如果当前节点的值小于待插入值，移动到右子树。
   • 如果当前节点的值大于待插入值，移动到左子树。
3. 插入新节点：
   • 根据比较结果，将新节点插入到 parent 的左孩子或右孩子位置。

因此，我们可以写出如下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

// bstree.hpp
template<typename T, typename CompFunc>
bool BST<T, CompFunc>::insertNormal(const T& value)
{
    if (m_root == nullptr)
    {
        m_root = new Node(value);
        return true;
    }
    Node* parent = nullptr; 
    Node* cur = m_root;
    while (cur != nullptr) 
    {
        parent = cur;
        if (cur->data == value)
        {
            cout << "插入失败,插入的元素值不能重复" << endl;
            return false;
        }
        else if (m_comp(cur->data, value)) 
        {
            cur = cur->right; 
        }
        else
        {
            cur = cur->left; 
        }
    }
    if (m_comp(value, parent->data))
    {
        parent->left = new Node(value);
    }
    else
    {
        parent->right = new Node(value);
    }
    return true;
}

3.2.2 递归实现

根据上面 BST 类的定义可以看出，在进行节点递归插入的时候对 insert 函数进行了重载：

• 外部接口：void insert(const T& value)
• 内部接口：void insert(Node* root, const T& value)

因为在进行递归操作的时候，需要不停的对树中的节点进行切换，因此需要提供一个Node 类型的参数，又由于对树的操作是从根节点开始的，而我们定义的BST类的根节点是私有成员，在类外部不可见，因此在类中又提供了一个重载的外部接口insert，在外部接口insert中对内部接口insert进行调用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

// bstree.hpp
template<typename T, typename CompFunc>
void BST<T, CompFunc>::insert(const T& value)
{
    m_root = insert(m_root, value);
}

template<typename T, typename CompFunc>
typename BST<T, CompFunc>::Node* BST<T, CompFunc>::insert(Node* root, const T& value)
{
    // 空树
    if (root == nullptr)
    {
        return new Node(value);
    }
    // 和当前节点值相同, 不允许插入
    if(root->data == value)
    {
        return root;
    }
    else if (m_comp(root->data, value))
    {
        root->right = insert(root->right, value);
    }
    else
    {
        root->left = insert(root->left, value);
    }
    return root; 
}

将新节点添加到二叉搜索树的核心思想如下：

1. 递归的返回值：

   • 在递归插入操作中，每次递归调用都会返回当前子树的根节点。
   • 对于非空节点，返回的是当前节点本身（root），目的是为了保持当前子树的结构不变。
   • 对于空节点，返回的是新创建的节点，这个节点会被赋值给其父节点的左指针或右指针。

2. 维护树的结构：返回 root 的目的是将新节点连接到其父节点的左子树或右子树。

   • 如果插入到右子树，root->right = insert(root->right, value)，返回的 root 会更新右子树的指针。
   • 如果插入到左子树，root->left = insert(root->left, value)，返回的 root 会更新左子树的指针。

3. 递归的终止条件：当递归到空节点时，返回新创建的节点，这个节点会被赋值给其父节点的左指针或右指针。

   1 2 3 4

   if (root == nullptr) { return new Node(value); // 返回新节点 }

关于第二个重载函数insert的返回值的语法问题，typename BST<T, CompFunc>::Node* 这种语法用于表示嵌套依赖类型。关于它的一些细节总结如下：

1. 嵌套依赖类型

   在 C++ 中，嵌套依赖类型是指模板类或模板函数中，依赖于模板参数的类型。这些类型通常是嵌套在模板类中的成员类型，或者是通过模板参数间接定义的类型。

   在这里，BST<T, CompFunc>::Node 是一个嵌套依赖类型。编译器在解析代码时无法直接确定 Node 是一个类型还是一个成员变量或其他内容，因为模板参数 T 和 CompFunc 是未知的。为了告诉编译器 Node 是一个类型，而不是其他东西，必须使用 typename 关键字。

   1 2 3 4 5

   template<typename T, typename CompFunc> typename BST<T, CompFunc>::Node* BST<T, CompFunc>::queryNormal(const T& value) { // ... }

   • BST<T, CompFunc> 是一个模板类。
   • Node 是 BST<T, CompFunc> 的嵌套类型。

2. 关于 typename 关键字的说明

   在模板中，编译器无法确定嵌套依赖类型是一个类型还是一个成员变量，因为在模板中类型和函数的确定会延迟到模板实例化时，所以代码生成是延迟的。因此，必须使用 typename 关键字来明确告诉编译器这是一个类型。例如：

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

   template<typename T> class MyClass { public: using value_type = T; // 定义 value_type 为 T 的别名 T value; }; template<typename T> void foo() { typename T::value_type x; // 等价于 T x; x = 10; std::cout << "x: " << x << std::endl; } int main() { foo<MyClass<int>>(); // T::value_type 是 int return 0; }

   1. typename 只能用于嵌套依赖类型：如果类型不依赖于模板参数，则不需要使用 typename。
   2. typename 不能用于非类型成员：例如，typename T::value 是错误的，因为 value 是一个成员变量，而不是类型。
   3. typename 和 class 的区别：在模板参数中，typename 和 class 可以互换，但在嵌套依赖类型中，只能使用 typename。

   当 foo 函数被调用时，模板参数 T 会被具体化。在这里：

   1 2 3 4 5

   int main() { foo<MyClass<int>>(); // T 被实例化为 MyClass<int> return 0; }

   • T 是 MyClass<int>，因此 T::value_type 是 int。
   • typename T::value_type x; 等价于 int x;。

3.3 删除操作

从二叉搜索树中删除一个值为 value 的节点。删除过程中需要处理三种不同的情况：

1. 情况1：待删除节点没有子节点（叶子节点）。
2. 情况2：待删除节点只有一个子节点。
3. 情况3：待删除节点有两个子节点。

3.3.1 非递归实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

// bstree.hpp
template<typename T, typename CompFunc>
bool BST<T, CompFunc>::removeNormal(const T& value)
{
    // 空树
    if (m_root == nullptr)
    {
        return false;
    }
    // 搜索待删除节点
    Node* cur = m_root;
    while (cur != nullptr && cur->data != value)
    {
        if (m_comp(cur->data, value)) 
        {
            cur = cur->right;
        }
        else
        {
            cur = cur->left;
        }
    }
    if (cur == nullptr)
    {
        return false;
    }
    Node* parent = nullptr;
    if (cur->left != nullptr && cur->right != nullptr)
    {
        parent = cur;
        Node* prev = cur->left;
        while (prev->right != nullptr)
        {
            parent = prev;
            prev = prev->right;
        }
        cur->data = prev->data;
        cur = prev; 
    }
    Node* child = cur->left;
    if (child == nullptr)
    {
        child = cur->right;
    }
    // 如果删除的是根节点
    if (parent == nullptr)
    {
        m_root = child;
    }
    else
    {
        if (parent->left == cur)
        {
            parent->left = child;
        }
        else
        {
            parent->right = child;
        }
    }
    delete cur;
    return true;
}

在上面的示例代码中，函数的具体处理流程如下：

1. 检查空树

   • 如果树为空（m_root 为 nullptr），直接返回 false，表示删除失败。

2. 搜索待删除节点

   • 从根节点开始，使用比较函数 m_comp 查找值为 value 的节点。

   • m_comp(cur->data, value) 返回 true 表示 cur->data < value，因此向右子树搜索；否则向左子树搜索。

3. 检查是否找到待删除节点

   • 如果没有找到值为 value 的节点，返回 false，表示删除失败。

4. 处理情况3（待删除节点有两个子节点）

   • 如果待删除节点有两个子节点，找到其左子树中的最大节点（前驱）或右子树中的最小节点（后继）。

   • 这里选择左子树的最大节点（前驱），通过不断向右遍历左子树找到。

   • 将前驱节点的值覆盖到待删除节点，然后将 cur 指向前驱节点。这样，问题转化为删除前驱节点（前驱节点最多只有一个子节点，即情况1或2）。

5. 处理情况1或2（待删除节点有一个或没有子节点）

   • 找到待删除节点的子节点（情况2）。

     • 如果左子节点存在，child 指向左子节点。
     • 如果左子节点不存在，child 指向右子节点。

   • 如果左右子节点都不存在，child 为 nullptr（情况1）。

6. 调整父节点指针

   • 如果待删除节点是根节点（parent 为 nullptr），直接将根节点指向 child。

   • 否则，根据待删除节点是父节点的左子节点还是右子节点，将父节点的指针指向 child。

7. 删除节点

   • 释放待删除节点的内存。

   • 返回 true，表示删除成功。

3.3.2 递归实现

与上面的非递归删除相比，使用递归方式实现代码更加简洁，逻辑更清晰。以下是示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

// bstree.hpp
template<typename T, typename CompFunc>
void BST<T, CompFunc>::remove(const T& value)
{
    m_root = remove(m_root, value);
}

template<typename T, typename CompFunc>
typename BST<T, CompFunc>::Node* BST<T, CompFunc>::remove(Node* root, const T& value)
{
    // 空树
    if (root == nullptr)
    {
        return nullptr;
    }
    // 找到了待删除节点
    if (root->data == value)
    {
        if (root->left != nullptr && root->right != nullptr)
        {
            Node* prev = root->left;
            while (prev->right != nullptr)
            {
                prev = prev->right; 
            }
            root->data = prev->data;
            root->left = remove(root->left, prev->data);
        }
        else
        {
            if (root->left != nullptr)
            {
                Node* left = root->left;
                delete root;
                return left;
            }
            else if (root->right != nullptr)
            {
                Node* right = root->right;
                delete root;
                return right;
            }
            else
            {
                delete root;
                return nullptr;
            }
        }
    }
    else if (m_comp(root->data, value))
    {
        root->right = remove(root->right, value); 
    }
    else
    {
        root->left = remove(root->left, value);
    }
    return root;
}

• 函数1：remove(const T& value)

  • 这是外部调用的接口函数，接收要删除的值 value。
  • 调用内部递归函数 remove(Node* root, const T& value)，从根节点开始查找并删除节点。
  • 更新根节点 m_root 为删除操作后的新根节点。

• 函数2：remove(Node* root, const T& value)

  • 这是递归删除的核心函数。

递归删除二叉搜索节点的具体流程如下：

1. 检查空树：

   • 如果当前子树为空（root 为 nullptr），直接返回 nullptr，表示没有找到要删除的节点。

2. 查找待删除节点

   • 如果当前节点的值等于 value，进入删除逻辑。

   • 如果当前节点的值小于 value，递归查找右子树。

   • 如果当前节点的值大于 value，递归查找左子树。

3. 处理删除逻辑

   1. 情况3：待删除节点有两个子节点

      • 如果待删除节点有两个子节点，找到其左子树中的最大节点（前驱）或右子树中最小节点（后继）。
      • 用前驱节点（或后继节点）的值覆盖待删除节点的值。
      • 递归删除前驱（或者后继）节点（此时前驱/后继节点最多只有一个子节点，即情况1或2）。

   2. 情况1或2：待删除节点有一个或没有子节点

      • 如果待删除节点只有左子节点，删除当前节点并返回左子节点。
        • 如果待删除节点只有右子节点，删除当前节点并返回右子节点。
        • 如果待删除节点没有子节点（叶子节点），删除当前节点并返回 nullptr。

4. 返回当前子树的根节点

   • 返回当前子树的根节点，用于更新父节点的指针。

3.4 查找操作

3.4.1 非递归实现

在二叉搜索树中查找一个值为 value 的节点，并返回指向该节点的指针。如果未找到，则返回 nullptr。

非递归查找示例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

// bstree.hpp
template<typename T, typename CompFunc>
typename BST<T, CompFunc>::Node* BST<T, CompFunc>::queryNormal(const T& value)
{
    // 从根节点开始遍历
    Node* cur = m_root;
    while (cur != nullptr)
    {
        if (cur->data == value)
        {
            return cur;
        }
        else if (m_comp(cur->data, value))  // 当前节点值小于参数value
        {
            cur = cur->right;
        }
        else
        {
            cur = cur->left;
        }
    }
    return nullptr;
}

查找函数的处理流程分为以下几步：

1. 初始化变量指针：从根节点 m_root 开始遍历。
2. 遍历树，比较当前节点的值：
   • 如果当前节点的值等于 value，找到了指定的节点。
   • 如果当前节点的值小于 value（m_comp(cur->data, value) 返回 true），向右子树搜索。
   • 如果当前节点的值大于 value，向左子树搜索。
   • 如果遍历到 nullptr，表示未找到值为 value 的节点。
3. 返回结果
   • 找到了，返回值为 value 的节点。
   • 没有找到，返回 nullptr。

3.4.2 递归实现

二叉树搜索树的递归查找示例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

// bstree.hpp
template<typename T, typename CompFunc>
typename BST<T, CompFunc>::Node* BST<T, CompFunc>::query(const T& value)
{
    return query(m_root, value);
}

template<typename T, typename CompFunc>
typename BST<T, CompFunc>::Node* BST<T, CompFunc>::query(Node* root, const T& value)
{
    // 空树
    if (root == nullptr)
    {
        return nullptr;
    }
    if (root->data == value)
    {
        return root;    // 找到了
    }
    else if (m_comp(root->data, value))
    {
        return query(root->right, value);
    }
    else
    {
        return query(root->left, value);
    }
}

• 函数1：query(const T& value)

  • 这是外部调用的接口函数，接收要查找的值 value。
  • 调用内部递归函数 query(Node* root, const T& value)，从根节点开始查找。

• 函数2：query(Node* root, const T& value)

  • 检查空树

    • 如果当前子树为空（root 为 nullptr），直接返回 nullptr，表示未找到目标节点。

  • 比较当前节点的值

    • 如果当前节点的值等于 value，返回当前节点指针。

    • 如果当前节点的值小于 value（m_comp(root->data, value) 返回 true），递归查找右子树。

    • 如果当前节点的值大于 value，递归查找左子树。

3.5 中序遍历

对二叉搜索树进行中序遍历就会得到一个升序的序列，中序遍历的顺序为：左子树 -> 根节点 -> 右子树。对应的代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

// bstree.hpp
template<typename T, typename CompFunc>
void BST<T, CompFunc>::inorder()
{
    cout << "中序遍历二叉搜索树: ";
    inorder(m_root);
    cout << endl;
}

template<typename T, typename CompFunc>
void BST<T, CompFunc>::inorder(Node* root)
{
    if (root == nullptr)
    {
        return;
    }
    inorder(root->left);
    cout << root->data << " ";
    inorder(root->right);
}

4. 测试

在一个新的源文件里，我们可以编写如下代码测试一下编写的二叉排序树类中的相关API函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

// test.cpp
#include "bstree.hpp"

int main()
{
    BST<int> tree;
    vector<int> data = { 33,2,4,9,1,6,45,77,55,39,35 };
    for (int i = 0; i < data.size(); ++i)
    {
        //tree.insertNormal(data.at(i));    // 非递归插入
        tree.insert(data.at(i));            // 递归插入
    }
    tree.inorder();
#if 0
    tree.removeNormal(9);
    tree.removeNormal(77);
    tree.removeNormal(45);
#else
    tree.remove(9);
    tree.remove(77);
    tree.remove(45);
#endif
    tree.inorder();
    //BST<int>::Node* node = tree.queryNormal(9);
    BST<int>::Node* node = tree.query(55);
    if (node != nullptr)
    {
        cout << "搜索到的节点值: " << node->data << endl;
    }
    else
    {
        cout << "没有找到指定的节点" << endl;
    }
    return 0;
}

终端打印结果如下:

1
2
3

中序遍历二叉搜索树: 1 2 4 6 9 33 35 39 45 55 77
中序遍历二叉搜索树: 1 2 4 6 33 35 39 55
搜索到的节点值: 55