B树、B+树

苏丙榅2025-03-092025-07-14

1. 2-3树

1.1 2-3树的特点

2 - 3树是一种自平衡的搜索树，属于多路搜索树，它在计算机科学领域有着广泛的应用，尤其在文件系统和数据库系统中用于高效的数据存储和检索。

2 - 3树是一种阶为3的B树，即每个节点最多有3个子节点。它可以包含两种类型的节点：

2 - 节点：包含一个键和两个子节点（左子节点和右子节点）。
1. 左子节点的所有键都小于该节点的键，右子节点的所有键都大于该节点的键。
2. 2节点要么没有孩子，要么有两个孩子，不能只有一个孩子
3 - 节点：包含两个键（键1和键2，且键1 < 键2）和三个子节点（左子节点、中间子节点和右子节点）。
1. 左子节点的所有键都小于键1，中间子节点的所有键都介于键1和键2之间，右子节点的所有键都大于键2。
2. 3节点要么没有孩子，要么有三个孩子，不存在有一个孩子或者两个孩子的情况
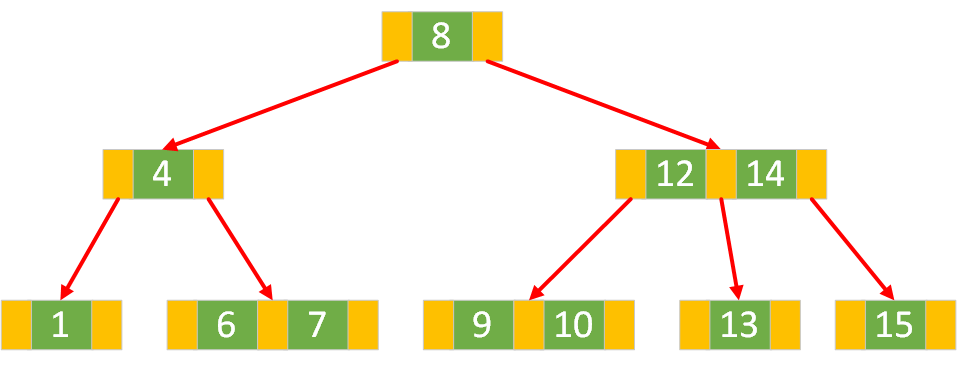
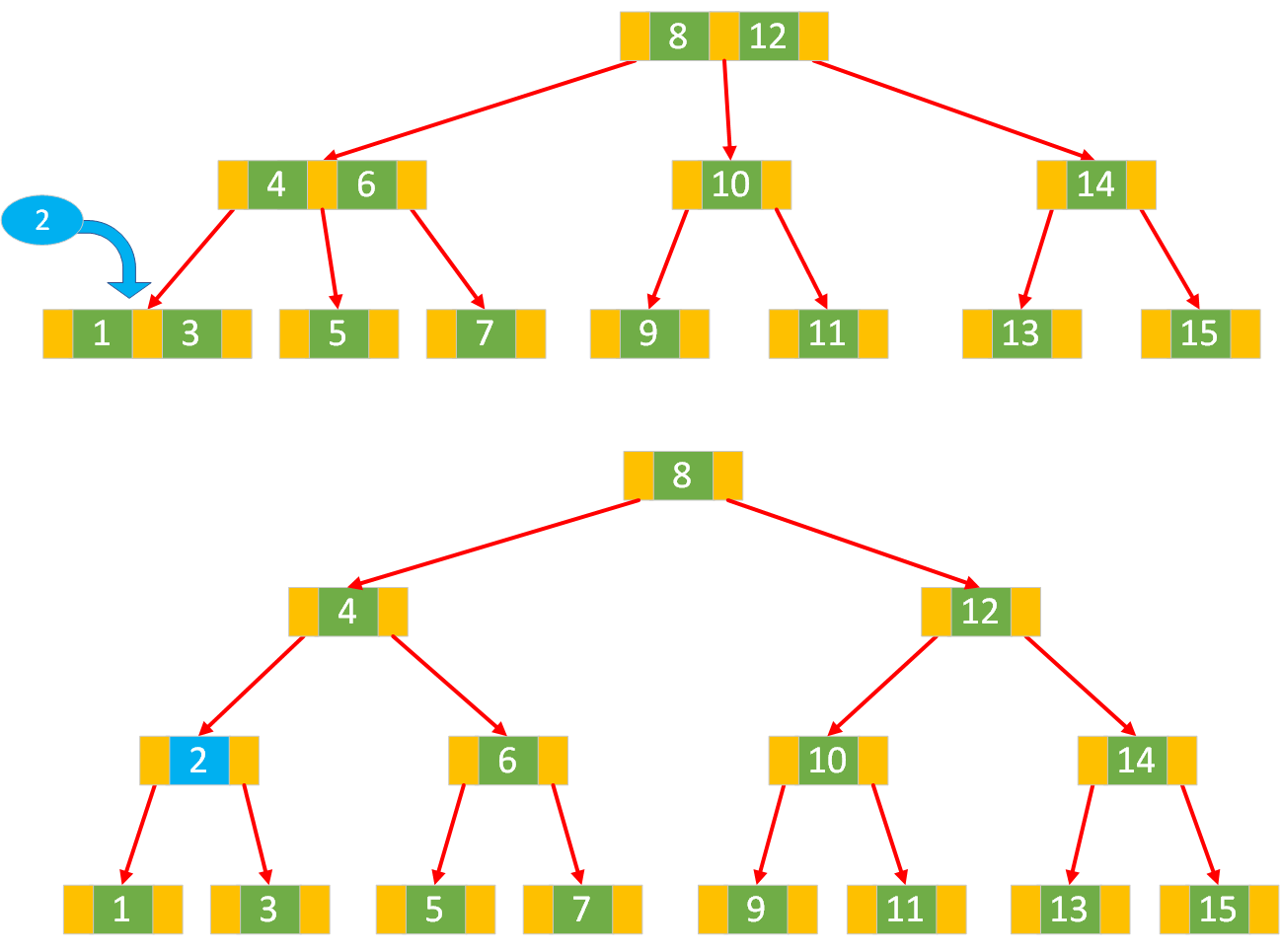
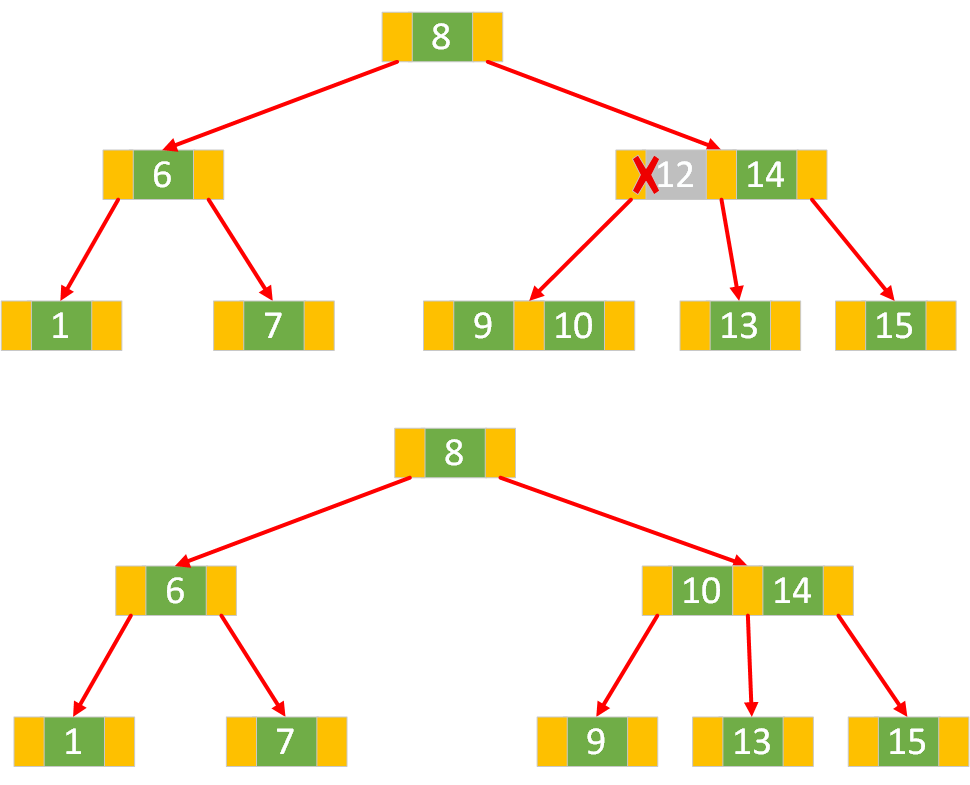
- 2-节点（8）：有一个数据域8和两个指针域，左子树4小于8，右子树12、14大于8
- 3节点（12、14）：有两个数据域12和14以及3个指针域，左子树9、10小于12，中子树13介于12和14之间，右子树15大于12和14
- 2-3 树的所有叶子节点都位于同一层次。

2 - 3 树是一种绝对平衡的树结构，即从根节点到树中任意一个叶子节点的路径长度都是相等的。这意味着树的高度是均匀的，不会出现某些分支过长而导致搜索效率降低的情况。无论数据如何插入或删除，树始终能保持这种平衡状态，从而保证了各种操作的时间复杂度相对稳定。

1.2 2-3树的数据搜索

2 - 3 树是一种自平衡的搜索树，它的节点可以是 2 节点（包含 1 个键和 2 个子节点）或 3 节点（包含 2 个键和 3 个子节点）。搜索的整体思路是：从树的根节点开始，根据当前节点的键与要搜索的键的大小关系，决定是向左子树、中间子树（如果是 3 节点）还是右子树继续搜索，直到找到目标键或者到达叶子节点仍未找到。

下面是在 2 - 3 树中进行数据搜索的详细步骤：

从根节点开始：将搜索指针指向 2 - 3 树的根节点。
判断当前节点类型及比较键的大小
- 如果当前节点是 2 节点：
  - 该节点包含一个键 key1 和两个子节点 left 和 right。
  - 比较要搜索的键targetKey 与key1的大小：
    - 若 targetKey == key1：搜索成功，返回该节点。
    - 若 targetKey < key1：将搜索指针移动到左子节点 left，继续进行搜索。
    - 若 targetKey > key1：将搜索指针移动到右子节点 right，继续进行搜索。
- 如果当前节点是 3 节点：
  - 该节点包含两个键 key1 和 key2（key1 < key2）以及三个子节点 left、middle 和 right。
  - 比较要搜索的键targetKey与key1和key2的大小：
    - 若 targetKey == key1 或 targetKey == key2：搜索成功，返回该节点。
    - 若 targetKey < key1：将搜索指针移动到左子节点 left，继续进行搜索。
    - 若 key1 < targetKey < key2：将搜索指针移动到中间子节点 middle，继续进行搜索。
    - 若 targetKey > key2：将搜索指针移动到右子节点 right，继续进行搜索。
重复步骤 2：不断重复步骤 2，沿着树的路径向下搜索，直到满足以下两种情况之一：
- 找到目标键：在某个节点中找到了与 targetKey 相等的键，此时搜索成功，返回该节点。
- 到达叶子节点仍未找到：当搜索指针到达叶子节点（没有子节点的节点）且该节点中没有与 targetKey 相等的键时，搜索失败，返回 null 或相应的表示未找到的标识。

1.3 2-3树的数据插入

2 - 3 树是一种自平衡的搜索树，插入操作需要保证树的平衡性质以及节点的规则（2 节点含 1 个键和 2 个子节点，3 节点含 2 个键和 3 个子节点）。以下是 2 - 3 树数据插入的具体步骤：

查找插入位置：从根节点开始，按照搜索规则查找要插入键的合适位置。
- 若当前节点是 2 节点（含 1 个键k1）：
  - 若待插入键 newKey < k1，则进入该节点的左子节点继续查找。
  - 若 newKey > k1，则进入该节点的右子节点继续查找。
- 若当前节点是 3 节点（含 2 个键k1和k2，且k1 < k2）：
  - 若 newKey < k1，则进入该节点的左子节点继续查找。
  - 若 k1 < newKey < k2，则进入该节点的中间子节点继续查找。
  - 若 newKey > k2，则进入该节点的右子节点继续查找。

不断重复上述过程，直到到达叶子节点，因为 2 - 3 树的插入操作总是在叶子节点进行。

插入键到叶子节点
1. 如果是空树，插入一个 2 节点，插入操作完成。
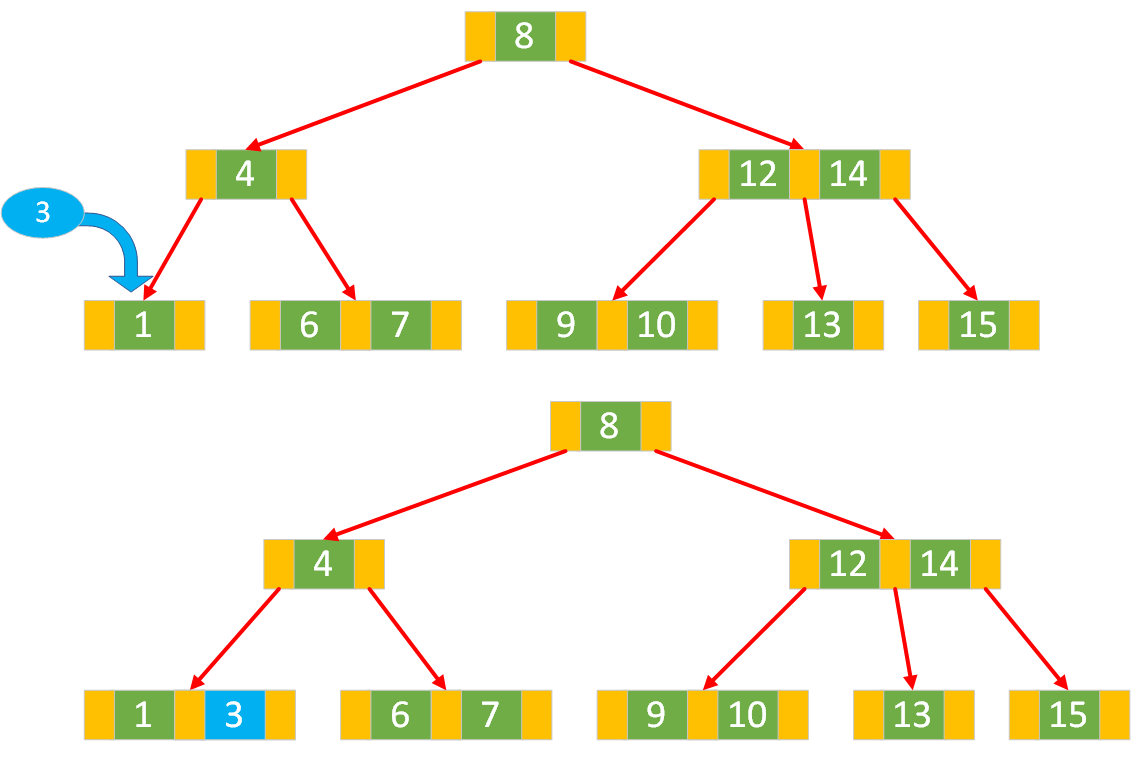
2. 叶子节点是 2 节点：若当前叶子节点是 2 节点，直接将新键插入到该节点中，并将键按升序排列。
  
  例如，原 2 节点键为 [k1]，插入 newKey 后，若 newKey < k1，节点变为 [newKey, k1]；若 newKey > k1，节点变为 [k1, newKey]。此时插入操作完成，树的结构无需进一步调整。
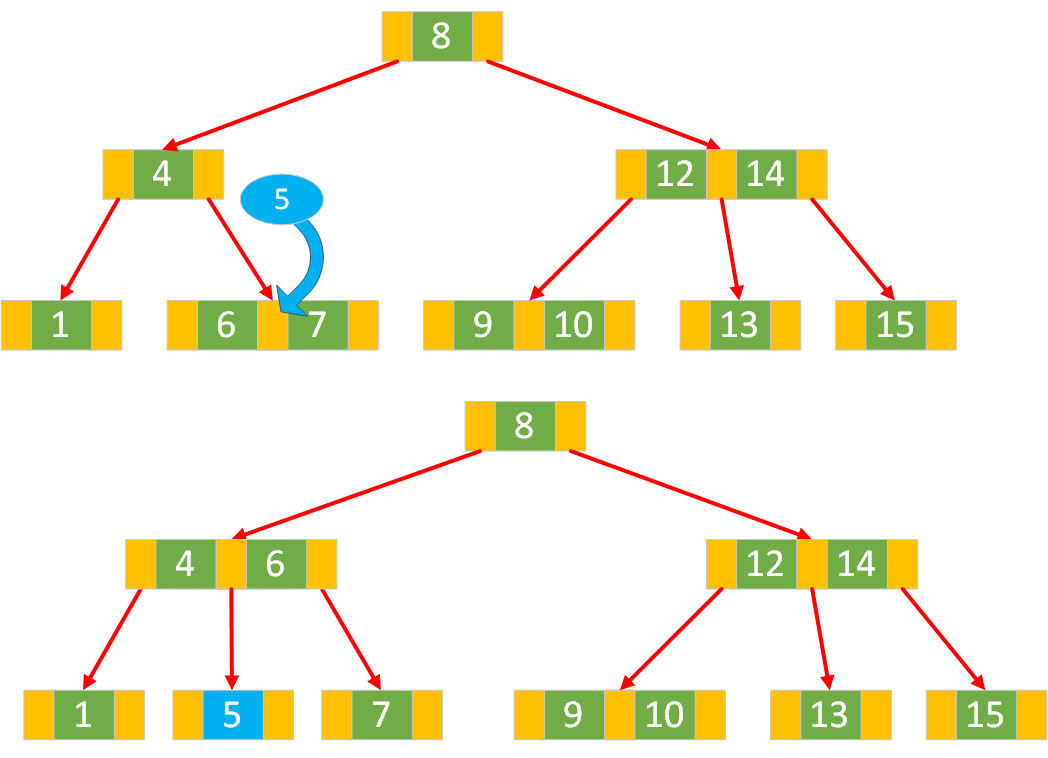
- 叶子节点是 3 节点：
  
  若当前叶子节点是 3 节点（键为[k1, k2]），插入新键newKey会导致节点溢出。需要进行节点分裂操作，具体步骤如下：
  1. 将新键插入到该节点中，并将所有键按升序排列，此时节点有 3 个键，如 [a, b, c]（a < b < c），此时得到一个 4 - 节点（可以存储3个键值，4个孩子）。
  2. 将 4-节点转换为一个棵由 3 个 2- 节点组成的 2-3 树
    - 创建两个新的 2 节点：一个节点包含键 [a]，另一个节点包含键 [c]。
    - 把中间的键 b 提升到父节点中。
处理父节点的插入和可能的分裂
- 父节点是 2 节点：
  
  若父节点是 2 节点，将从子节点提升上来的键插入到父节点中，并将父节点的子指针进行相应调整。例如，原父节点为 [p1]，子节点分裂后提升键 b 插入，若 b < p1，父节点变为 [b, p1]，同时调整子指针；若 b > p1，父节点变为 [p1, b]，并调整子指针。插入操作完成，树的结构调整结束。
- 父节点是 3 节点：
  
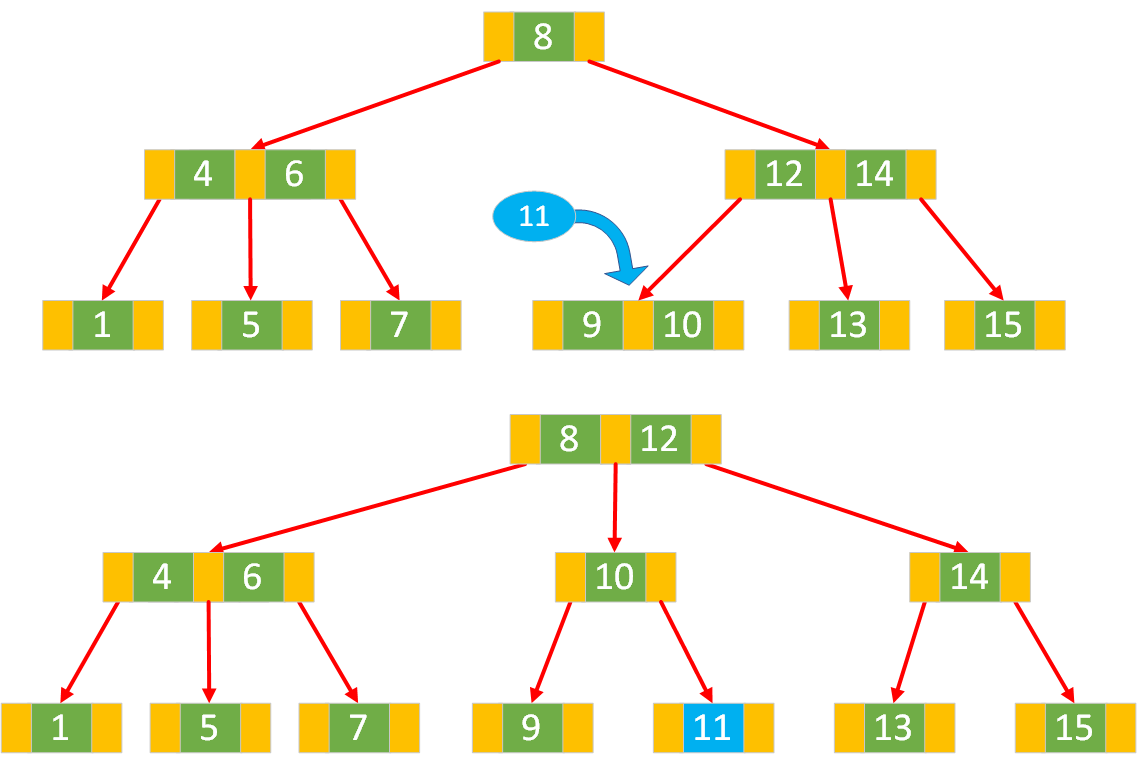
  若父节点是 3 节点，插入从子节点提升上来的键会导致父节点溢出，需要对父节点进行分裂。过程与叶子节点分裂类似：
  1. 将提升上来的键插入到父节点中，并将所有键按升序排列。
  2. 创建两个新的 2 节点，分别包含部分键。
  3. 把中间的键提升到父节点的父节点中。
处理根节点的分裂：

若分裂操作一直向上传播到根节点，且根节点也是 3 节点，插入提升上来的键后根节点溢出，需要对根节点进行分裂：
- 创建两个新的 2 节点，分别包含部分键。
- 创建一个新的根节点，该根节点为 2 节点，包含从原根节点分裂出来的中间键，并且新根节点的两个子指针分别指向两个新创建的 2 节点。此时树的高度增加 1。

1.4 2-3树的数据删除

2 - 3 树的数据删除操作相对复杂，需要保证树的平衡性质以及节点的规则（2 节点含 1 个键和 2 个子节点，3 节点含 2 个键和 3 个子节点）。以下是 2 - 3 树数据删除的具体步骤：

查找要删除的键：从根节点开始，按照搜索规则查找要删除的键。
- 若当前节点是 2 节点（含 1 个键k1）：
  - 若要删除的键 deleteKey < k1，则进入该节点的左子节点继续查找。
  - 若 deleteKey > k1，则进入该节点的右子节点继续查找。
  - 若 deleteKey == k1，则找到了要删除的键。
- 若当前节点是 3 节点（含 2 个键k1和k2，且k1 < k2）：
  - 若 deleteKey < k1，则进入该节点的左子节点继续查找。
  - 若 k1 < deleteKey < k2，则进入该节点的中间子节点继续查找。
  - 若 deleteKey > k2，则进入该节点的右子节点继续查找。
  - 若 deleteKey == k1 或 deleteKey == k2，则找到了要删除的键。
删除键的情况处理
- 情况一：要删除的键在叶子节点
  - 叶子节点是 3 节点：若要删除的键所在的叶子节点是 3 节点，直接从该节点中删除该键，然后将剩余的键按升序排列。
    
    例如，原 3 节点键为 [k1, k2]，若删除 k1，节点变为 [k2]；若删除 k2，节点变为 [k1]。此时删除操作完成，树的结构无需进一步调整。
  - 叶子节点是 2 节点：若要删除的键所在的叶子节点是 2 节点，直接删除该键会导致节点下溢（节点键数不足），需要进行节点合并或借键操作，具体如下：
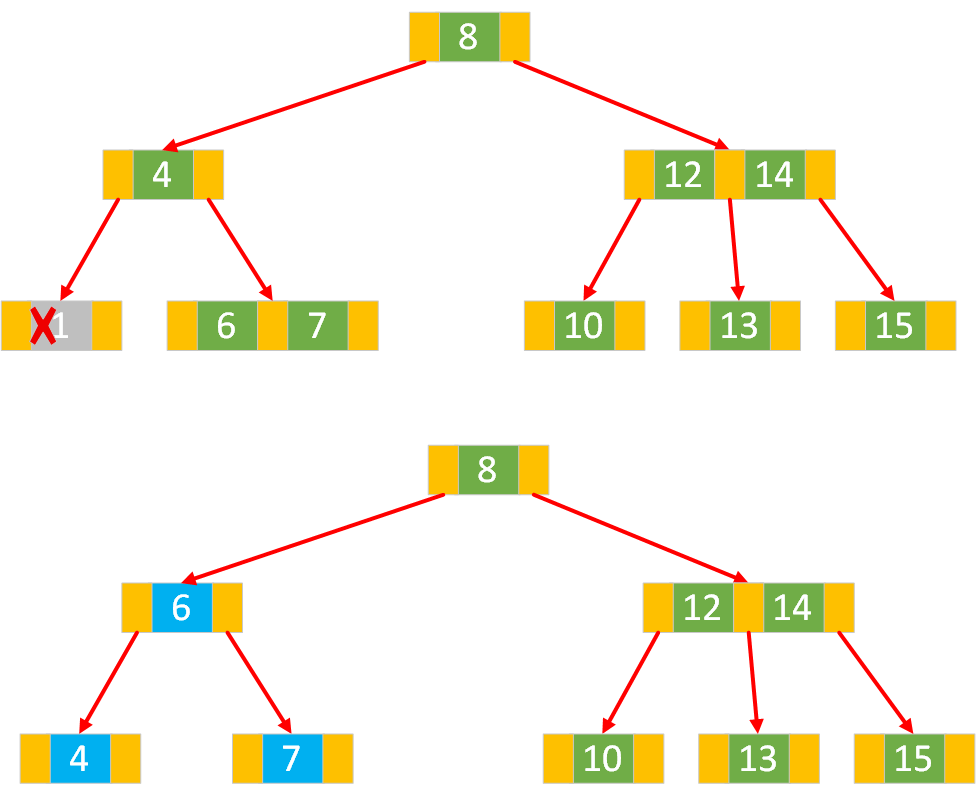
    - 情形1：此节点的父节点是 2 节点，兄弟是 3 节点。
      - 左兄弟节点是 3 节点：将左兄弟节点的最大键移动到父节点，再将父节点中对应分隔该节点和左兄弟节点的键移动到该节点。
      - 右兄弟节点是 3 节点：将右兄弟节点的最小键移动到父节点，再将父节点中对应分隔该节点和右兄弟节点的键移动到该节点。
    - 情形2：此节点的父节点是 2 节点，兄弟也是 2 节点。
      
      当前待删除节点的父节点是2-节点、兄弟节点也是2-节点，先通过移动兄弟节点的中序遍历直接后继到兄弟节点，以使兄弟节点变为3-节点；
      
      接下来再次按照情形1进行操作，就完成了节点的删除。
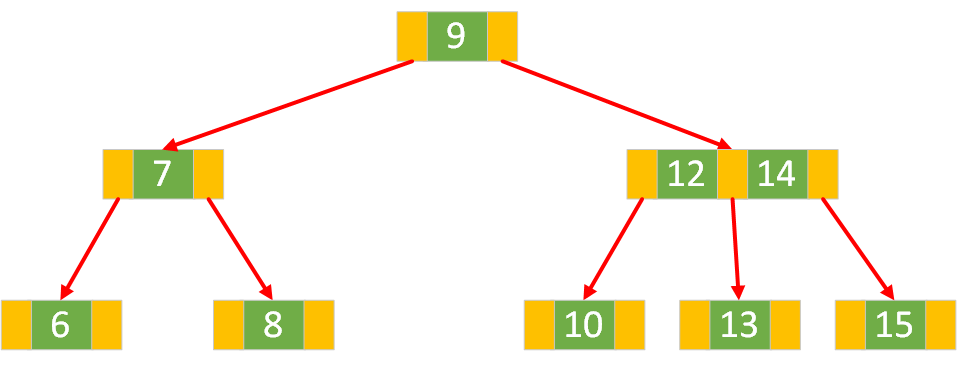
  - 情形3：此节点的父节点是 3 节点
    
    当前待删除节点的父节点是3-节点，拆分父节点使其成为2-节点，再将父节点中最接近的一个值与中孩子合并。
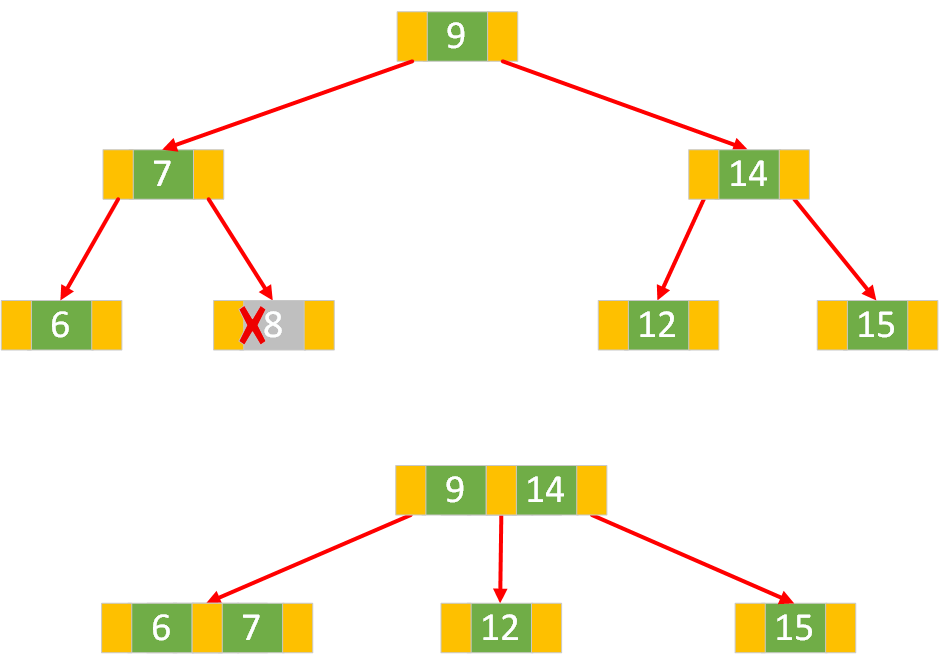
  - 2-3树为满二叉树，删除叶子节点
    
    若2-3树是一颗满二叉树，将2-3树层树减少，并将当前删除节点的兄弟节点合并到父节点中，同时将父节点的所有兄弟节点合并到父节点的父节点中。
- 情况二：要删除的键在非叶子节点
  
  使用中序遍历下的直接后继（或直接前驱）节点值来覆盖当前待删除节点的值，再删除用来值覆盖的后继节点（或前驱节点）。
  
  删除后继节点的操作:
  
  删除前驱节点的操作:

2. B树

B树是一种自平衡的多路搜索树，它具有多种重要属性，这些属性保证了其在数据存储和检索方面的高效性。下面从阶数、节点结构、高度平衡、键的有序性为大家做详细介绍：

阶数（Degree）
- 定义：B树的阶数用 m 表示，它决定了每个节点可以容纳的键和子节点的数量范围。
- 节点键数量限制：除根节点外，每个内部节点至少包含 ⌈m/2⌉ - 1 个键，最多包含 m - 1 个键。
  - ⌈ ⌉ 表示向上取整，向上取整 ⌈1.5⌉ = 2
  - 根节点如果不是叶子节点，至少有 1 个键、两棵子树；
  - 根节点为叶子节点，则可以有 0 到 m - 1 个键。
- 子节点数量限制：每个内部节点的子节点数量比键的数量多 1。
  - 除根节点外，内部节点的子节点数量在 ⌈m/2⌉ 到 m 之间；
  - 根节点的子节点数量可以是 2 到 m 个。
节点结构
- 键：每个节点包含多个键，这些键按照升序排列。键用于对数据进行索引和查找。
- 子节点指针：每个内部节点包含多个子节点指针，用于指向子节点。子节点指针的数量比键的数量多 1，这些指针将节点的子树划分为不同的区间。
高度平衡
- B树的所有叶子节点都位于同一层，这保证了树的高度相对较低且平衡。无论从根节点到哪个叶子节点，路径长度都是相同的。这种高度平衡的特性使得B树在进行查找、插入和删除操作时，时间复杂度稳定在 O(log n)，其中 n 是树中键的总数。
键的有序性
- 节点内的键按升序排列，即对于节点中的任意两个键 key[i] 和 key[j]（i < j），都有 key[i] < key[j]。
- 子树之间也遵循有序性，对于一个内部节点的第 i 个键 key[i]，其左子树中的所有键都小于 key[i]，右子树中的所有键都大于 key[i]。

2.1 B树的节点插入

B树的节点插入流程和 2-3 树类似，比如现在有一棵 5 阶的B树，现有若干个节点，我们依次将其插入到这棵树中。

这棵 5 阶的B树初始状态为空，插入数据[1, 3, 7, 14]
插入数据[8]，得到一个 6 - 节点，将其进行分解，中间的 key 提升为父节点，树的高度增加 1。
插入数据[5, 11, 17]
插入数据[13]，右子树变为 6-节点，将其进行分解，中间 key（13）被提升为父节点，与原来的父节点合并
插入数据[6, 12, 20，23]
插入数据[26]，右子树变为 6-节点，将其进行分解，中间 key（20）被提升为父节点，与原来的父节点合并
插入数据[4]，左子树变为 6-节点，将其进行分解，中间 key（4）被提升为父节点，与原来的父节点合并
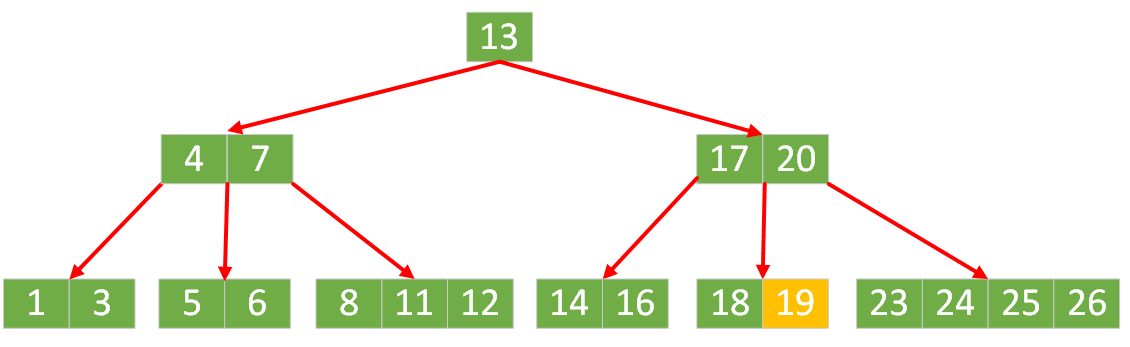
插入数据[16, 18, 24，25]
插入数据[19]，左4树变为 6-节点，将其进行分解，中间 key（17）被提升为父节点，与原来的父节点合并，此时父节点也变成了 6-节点，继续分解，中间 key（13）被提升为父节点，树的高度增加1。

2.2 B树的节点删除

现在我们上面构建的 5 阶B树为例，进行树节点的删除。

删除叶子节点【8】，直接删除即可。
删除非叶子节点【20】，找到该节点中序遍历的后继节点【23】，用后续节点值覆盖待删除节点值，并删除该后继节点。
删除叶子节点【18】，5阶B树的每个节点中最少存储的键值数量为 ⌈5/2⌉-1 = 3-1 = 2。删除节点【18】之后剩余键值数量为 1，所以需要像兄弟借一个节点。
- 从右兄弟节点中选出最小的 key 值给到父节点
- 从父节点中选出 key 值位于中子树和右子树中间的节点【23】给到中子树节点按大小顺序进行合并
删除叶子节点【5】，5阶B树的每个节点中最少存储的键值数量为 ⌈5/2⌉-1 = 3-1 = 2。删除节点【18】之后剩余键值数量为 1，并且该中子树的左右兄弟都没有多余的节点可借，此时需要合并兄弟节点。
- 合并左子树节点【1,3】和中子树节点【6】，位于二者中间的父节点【4】需要下移
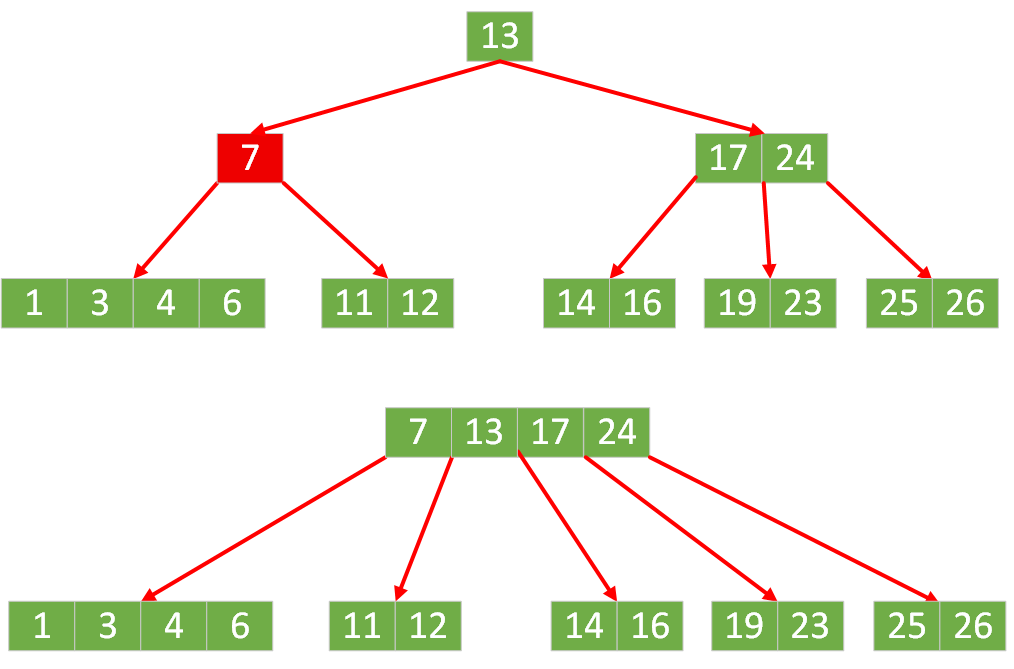
- 非叶子节点叶子节点【7】中存储的键值不满足 5 阶B树的每个节点中最少存储的键值数量 ⌈5/2⌉-1 = 3-1 = 2，需要继续合并节点【7】和其兄弟节点【17,24】，位于二者中间的父节点【13】需要下移，树高度减少 1。

2.3 B树的应用场景

B树是一种高效的数据结构，特别适合在磁盘存储和大规模数据访问的场景中使用。以下是一些主要的应用场景：

文件系统
- 数据组织与管理：文件系统需要高效地管理大量的文件和目录信息。B树可以将文件的元数据（如文件名、文件大小、创建时间等）存储在节点中，通过树结构组织这些数据。由于B树的节点可以存储多个键值对，能充分利用磁盘的块存储特性，减少磁盘I/O操作。例如，当查找一个文件时，可从根节点开始，根据文件名的比较结果快速定位到包含该文件信息的节点，大大提高了文件查找的速度。
- 空间分配与回收：文件系统要管理磁盘的存储空间，包括文件的分配和回收。B树可以用于记录磁盘块的使用情况，每个节点存储一定范围内磁盘块的使用状态。当需要分配新的磁盘块给文件时，能通过B树快速找到可用的磁盘块；当文件被删除时，也能迅速更新相应节点的信息，实现磁盘空间的高效回收。
数据库系统
- 索引结构：数据库系统经常需要对大量的数据进行查询、插入和删除操作。B树常被用作数据库索引的基础结构，如在关系型数据库MySQL中，InnoDB存储引擎的索引就是基于B+树（B树的一种变体）实现的。数据库中的表可能包含数百万甚至数十亿条记录，通过在表的某些列上创建B树索引，查询时可以避免全表扫描，直接根据索引定位到包含目标数据的磁盘块，极大地提高了查询效率。
- 事务处理：在数据库的事务处理中，需要快速地对数据进行读写操作。B树的平衡特性和高效的查找、插入、删除操作，能够保证在并发事务处理时，数据的一致性和操作的高效性。例如，在一个银行系统的数据库中，多个用户同时进行转账、查询余额等操作，B树索引可以帮助系统快速定位和更新相关账户的数据。
内存数据库
- 数据缓存：在内存数据库中，虽然数据存储在内存中，访问速度很快，但当数据量较大时，仍然需要一种高效的数据结构来组织和管理数据。B树可以作为内存数据库的数据缓存结构，将频繁访问的数据存储在B树中，通过B树的高效查找和插入操作，提高数据的访问效率。例如，一些内存数据库在处理复杂的查询时，使用B树来存储中间结果，减少了数据的重复计算和访问时间。
- 并发控制：内存数据库通常需要支持高并发的读写操作。B树的结构可以方便地实现并发控制机制，通过对节点的加锁操作，保证在多个线程或进程同时访问数据时的一致性和正确性。例如，在一个多用户的在线游戏中，内存数据库使用B树存储玩家的游戏数据，当多个玩家同时进行游戏操作时，B树的并发控制机制可以确保数据的完整性和操作的正确性。
磁盘存储系统
- 磁盘阵列管理：磁盘阵列（如RAID）是由多个磁盘组成的存储系统，需要对这些磁盘上的数据进行高效的管理。B树可以用于磁盘阵列的元数据管理，记录每个磁盘块在阵列中的位置和状态。当需要读取或写入数据时，通过B树可以快速定位到数据所在的磁盘和位置，提高了磁盘阵列的读写性能。
- 数据备份与恢复：在磁盘存储系统的备份和恢复过程中，B树可以用于管理备份数据的索引信息。备份数据可能包含大量的文件和目录，通过B树可以快速定位到需要备份或恢复的文件，减少备份和恢复的时间。例如，在企业级的磁盘存储系统中，定期进行数据备份时，使用B树管理备份文件的索引，当需要恢复数据时，可以迅速找到相应的备份文件进行恢复操作。

为什么在处理磁盘I/O的时候使用的是B树，而不是AVL树或者红黑树呢？

从磁盘 I/O 的方向解释，B 树的搜索效率通常比 AVL 树或者红黑树高，主要原因在于 B 树的设计更适合处理磁盘存储和大规模数据访问。以下是详细的解释（以 AVL 树为例和 B树进行对比）：

磁盘 I/O 的特点
- 访问速度慢：与内存相比，磁盘的访问速度非常慢，通常以毫秒（ms）为单位。
- 按块读取：磁盘读取数据时，通常以块（block）为单位，而不是单个字节或节点。
- 减少 I/O 次数是关键：为了优化性能，尽量减少磁盘 I/O 次数是设计数据结构时的重要目标。
B 树的设计优势

B 树是一种多路平衡搜索树，其设计非常适合磁盘存储，原因如下：
- 节点存储多个键值
  - B 树的每个节点可以存储多个键值（通常与磁盘块大小匹配），而不是像 AVL 树那样每个节点只存储一个键值。
  - 例如，一个 300 阶的 B 树，每个节点可以存储多达 300 个子节点指针和 299 个键值。
  - 这意味着一次磁盘 I/O 可以读取更多的数据，从而减少访问次数。
- 树的高度更低
  - B 树的分支因子（每个节点的子节点数）远大于 AVL 树（分支因子为 2），因此 B 树的高度更低。
    - 对于 10000000 条数据：
      - AVL 树的高度约为 34 层。
      - 300 阶 B 树的高度仅为 4 层。
  - 树的高度越低，搜索时需要的磁盘 I/O 次数越少。
- 减少磁盘寻址
  - B 树的结构使得每次磁盘 I/O 都能读取更多的数据，减少了磁盘寻址的开销。
  - 例如，在搜索时，B 树只需访问 4 个节点，而 AVL 树可能需要访问 34 个节点。
AVL 树的局限性

AVL 树是一种二叉平衡搜索树，其设计更适合内存中的数据操作，但在磁盘存储场景下存在以下问题：
- 每个节点存储一个键值
  - AVL 树的每个节点只存储一个键值，这意味着每次磁盘 I/O 只能读取一个节点的数据。
  - 对于大规模数据，这会导致大量的磁盘 I/O 操作。
- 树的高度较高
  - AVL 树的分支因子为 2，因此树的高度较高。
  - 对于 10000000 条数据，AVL 树的高度约为 34 层，搜索时需要访问更多的节点，导致更多的磁盘 I/O。
- 频繁的旋转操作
AVL 树在插入和删除时可能需要频繁的旋转操作以保持平衡，这会导致额外的磁盘 I/O 开销。
对比示例

假设每次磁盘 I/O 读取一个节点：
- B 树：高度为 4 层，搜索时最多需要 4 次磁盘 I/O。
- AVL 树：高度为 34 层，搜索时最多需要 34 次磁盘 I/O。

显然，B 树的磁盘 I/O 次数远低于 AVL 树，因此在磁盘存储场景下，B 树的搜索效率更高。

3. B+树

B+树是B树的一种变体，广泛应用于数据库和文件系统中，具有以下显著特点：

数据仅存储在叶子节点
- 内部节点只存储键：B+树的内部节点仅存储键，用于导航，不存储实际数据。
- 叶子节点存储数据：所有数据都存储在叶子节点中，叶子节点通过指针连接形成一个有序链表。
叶子节点链表连接
- 有序链表：所有叶子节点通过指针连接成一个有序链表，便于范围查询和顺序访问。
- 高效范围查询：由于叶子节点有序连接，范围查询时只需遍历链表，无需回溯树结构。
高效磁盘I/O
- 减少I/O次数：B+树的内部节点仅存储键，单个节点可以存储更多的键，从而减少树的高度和磁盘I/O次数。
- 块利用率高：由于数据集中在叶子节点中，块利用率较高，适合大规模数据存储。

3.1 B树和B+树的区别

B树和B+树都是多路平衡搜索树，广泛应用于数据库和文件系统中，但它们在结构和应用场景上有一些关键区别。以下是它们的详细对比：

结构差异
- B树
  - 节点存储数据：B树的每个节点（包括内部节点和叶子节点）都存储键值对。
  - 数据分布：数据分布在整棵树的各个节点中，查找时可能在任何节点找到目标数据。
  - 子节点数量：每个节点的子节点数量介于⌈m/2⌉和m之间（m为树的阶数）。
- B+树
  - 内部节点只存储键：B+树的内部节点只存储键，不存储数据，数据仅存储在叶子节点中。
  - 叶子节点链表：B+树的所有叶子节点通过指针连接成一个有序链表，便于范围查询。
  - 子节点数量：与B树类似，每个节点的子节点数量介于⌈m/2⌉和m之间。
数据存储方式
- B树
  - 数据分散存储：数据分布在整棵树的各个节点中，查找时可能在任何节点找到目标数据。
  - 查找效率：查找效率取决于目标数据所在的节点深度，可能在内部节点或叶子节点找到数据。
- B+树
  - 数据集中存储：数据仅存储在叶子节点中，内部节点只存储键用于导航。
  - 查找效率：查找效率较为稳定，因为无论目标数据是什么，都需要遍历到叶子节点。
查询性能
- B树
  - 点查询：由于数据分布在整棵树中，点查询的效率较高，可能在中途找到目标数据。
  - 范围查询：范围查询效率较低，因为需要遍历多个节点，且数据分布不连续。
- B+树
  - 点查询：点查询效率略低于B树，因为必须遍历到叶子节点才能找到数据。
  - 范围查询：范围查询效率高，因为叶子节点通过链表连接，可以快速遍历范围内的数据。
磁盘I/O性能
- B树
  - I/O次数：由于数据分布在整棵树中，查找过程中可能需要访问多个节点，导致磁盘I/O次数较多。
  - 块利用率：由于每个节点都存储数据，块利用率可能较低。
- B+树
  - I/O次数：由于内部节点只存储键，单个节点可以存储更多的键，树的高度和磁盘I/O次数减少。
  - 块利用率：由于数据集中在叶子节点中，块利用率较高。
应用场景
- B树
  - 适合点查询：适用于点查询较多的场景，如内存数据库或某些特定的文件系统。
  - 数据量较小：在数据量较小、树的高度较低时，B树的性能可能优于B+树。
- B+树
  - 适合范围查询：适用于范围查询较多的场景，如数据库索引和文件系统。
  - 数据量较大：在数据量较大、树的高度较高时，B+树的性能优于B树。

3.2 总结

特性	B树	B+树
数据存储位置	内部节点和叶子节点都存储数据	仅叶子节点存储数据
内部节点内容	存储键值对	仅存储键
叶子节点连接	无链表连接	通过链表连接
插入/删除	适合频繁更新	调整成本略高
范围查询效率	较低	较高
磁盘I/O性能	较差	较好
块利用率	较低	较高