霍夫曼树和霍夫曼编码

1. 霍夫曼树

霍夫曼树（Huffman Tree），又称最优二叉树，它是一种在给定一组带有特定权值的叶子节点后，构建出的带权路径长度（Weighted Path Length, WPL）达到最小的二叉树。

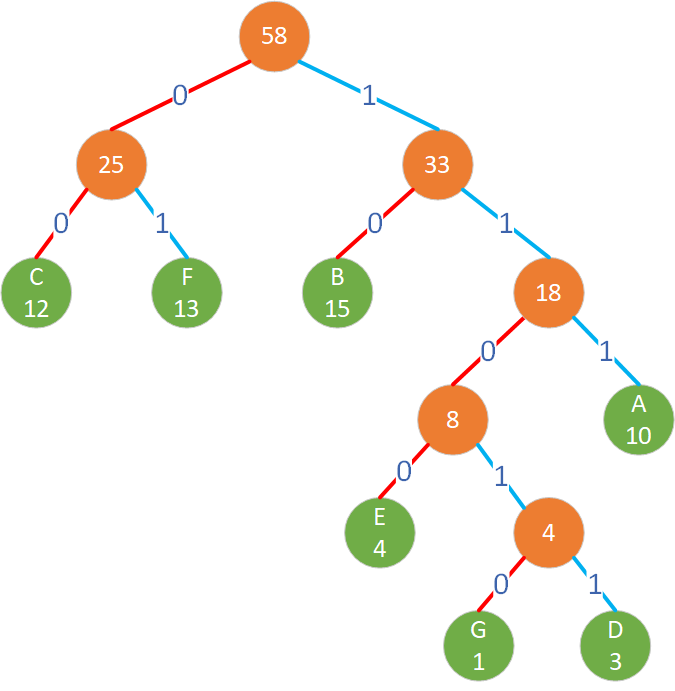
基于下表我们可以构建出这样一棵霍夫曼树：

数据 权值（频率）
A 10
B 15
C 12
D 3
E 4
F 13
G 1
image-20250220103947353

在学习霍夫曼树的过程中，有几个关键概念需要大家深入理解。接下来，我将为大家逐一详细介绍。

1.1 重要概念解析

字符频率

  • 定义：字符频率是指在一个数据集中，某个字符出现的次数或概率。
  • 作用：霍夫曼树的构建依赖于字符的频率，频率越高的字符在树中的路径越短，从而获得更短的编码。
  • 示例：在字符串 "aabbbcc" 中，字符 'a' 的频率为 2，'b' 的频率为 3，'c' 的频率为 2。

叶子节点

  • 定义：霍夫曼树中的叶子节点表示字符及其频率。
  • 作用：使用叶子节点存储字符及其频率信息。
  • 示例：在霍夫曼树中，字符 'a' 和 'b' 分别对应一个叶子节点。

内部节点

  • 定义：霍夫曼树中的内部节点表示两个子节点的合并。
  • 特点：
    • 内部节点不存储字符信息，只存储频率（权值）信息。
    • 内部节点的频率（权值）是其两个子节点频率（权值）之和。
  • 示例：如果一个内部节点的左子节点频率为 2，右子节点频率为 3，则该内部节点的频率为 5。

路径

  • 定义：路径是指从根节点到某个叶子节点的分支序列。
  • 特点：
    • 路径的长度决定了字符编码的长度。
    • 路径上的分支用 0 或 1 表示。
  • 示例：如果从根节点到字符 'a' 的路径是 左 -> 右 -> 左，则 'a' 的编码为 010。

编码规则

  • 定义：霍夫曼树的编码规则是左分支表示 0，右分支表示 1。
  • 作用：通过路径上的 0 和 1 序列生成字符的唯一编码。
  • 示例：如果从根节点到字符 'b' 的路径是 右 -> 左，则 'b' 的编码为 10。

优先队列

  • 定义：优先队列是一种数据结构，用于按优先级（如频率）存储节点。
  • 特点：
    • 在霍夫曼树中，优先队列通常是最小堆（Min-Heap），频率最小的节点优先出队。
    • 用于构建霍夫曼树时，每次取出两个频率最小的节点进行合并。
  • 示例：优先队列中存储了字符 'a'（频率 2）、'b'（频率 3）、'c'（频率 2），首先取出 'a' 和 'c'。

霍夫曼编码

  • 定义：霍夫曼编码是基于霍夫曼树生成的二进制编码，每个字符对应一个唯一的编码。
  • 特点：
    • 高频字符的编码较短，低频字符的编码较长。
    • 编码是前缀码（Prefix Code），即没有任何编码是其他编码的前缀。
  • 示例：字符 'a' 的编码为 0，字符 'b' 的编码为 10，字符 'c' 的编码为 11。

前缀码

  • 定义：前缀码是一种编码方式，其中没有任何编码是其他编码的前缀。
  • 特点：前缀码可以唯一解码，无需分隔符。
  • 示例：编码 0、10、11 是前缀码，因为没有任何编码是其他编码的前缀。

数据压缩

  • 定义：数据压缩是通过减少数据的存储空间来节省资源的过程。
  • 作用：霍夫曼树通过为字符分配最优编码，实现数据的高效压缩。
  • 示例：原始字符串 "aabbbcc" 的霍夫曼编码为 001010101111，比原始字符串的二进制表示更短。

无损压缩

  • 定义：无损压缩是一种压缩方式，压缩后的数据可以完全恢复为原始数据。
  • 特点：
    • 霍夫曼编码是无损压缩算法。
    • 适用于文本、代码等需要完全恢复的场景。

权值

  • 定义：赋予树中节点的一个数值，它代表了该节点在特定应用场景下的某种重要程度、频率或者代价等意义。不同的应用场景中，权值所代表的实际意义有所不同。

  • 权值的应用:

    • 数据压缩：权值表示对应字符在待编码数据中出现的频率

    • 决策树算法：权值可以表示某个特征或者属性的重要性

    • 通信传输：节点的权值可以表示传输某个信息所需的代价，比如时间、带宽等。

节点的带权路径长度

  • 定义：从该节点到树根之间的路径长度与该节点权值的乘积。
  • 计算公式：设节点的权值为 w，该节点到根节点的路径长度为 l，路径为p，则WPL = w * l
  • 示例：假设节点 A 的权值 wA=5，从节点 A到根节点要经过 3 条边，即路径长度 lA=3，那么节点 A的带权路径长度 WPLA=wA×lA=5×3=15

树的带权路径长度

  • 定义：树中所有叶子节点的带权路径长度之和。在霍夫曼树中，由于其构造目的就是使得这个值最小，所以它也被称为最优二叉树。

  • 示例：设有四个叶子节点 a、b、c、d，它们的权值分别为 wa=2=2、wb=3、wc=4、wd=5，对应的路径长度分别为 la=3、lb=3、lc=2、ld=2。则该霍夫曼树的带权路径长度为：

    WPL = wa×la + wb×lb + wc×lc + wd×ld=2×3+3×3+4×2+5×2=6+9+8+10=33

1.2 构建步骤

在处理文本或二进制数据时，我们首先需要知道每个字符（或字节）出现的频率。这是构建霍夫曼树的基础，因为后续节点的合并是基于频率进行的。霍夫曼树的构建步骤如下:

  1. 统计字符频率：遍历输入数据，统计每个字符出现的频率。
    • 遍历输入的字符串，使用一个 std::unordered_map 来记录每个字符出现的频率。
    • std::unordered_map 可以高效地进行查找和插入操作，其平均时间复杂度为 O(1)。
  2. 构建优先队列：将每个字符及其频率作为一个节点，放入优先队列（最小堆）中。
    • 优先队列（最小堆）可以使用 std::priority_queue 来实现。
    • 将每个字符及其频率封装成一个 HuffmanNode 对象，并将这些对象插入到优先队列中。
    • 优先队列会自动根据节点的频率进行排序，确保每次取出的都是频率最小的节点。
  3. 构建霍夫曼树：
    • 从优先队列中取出两个频率最小的节点，合并成一个新的节点，新节点的频率为两个子节点频率之和。
    • 将新节点放回优先队列。
    • 重复上述步骤，直到队列中只剩一个节点，该节点即为霍夫曼树的根节点。

2. 霍夫曼编码

霍夫曼编码（Huffman Coding）是一种用于无损数据压缩的算法。该算法的核心思想是通过构建霍夫曼树，将出现频率高的字符用较短的编码表示，出现频率低的字符用较长的编码表示，从而实现数据的压缩。在实际应用中，霍夫曼编码被广泛用于图像、音频和视频等数据的压缩。

2.1 编码

在对文本进行霍夫曼编码之前，首先需要统计文本中每个字符出现的频率。这一步骤可以帮助我们了解每个字符在文本中的重要性，为后续构建霍夫曼树提供基础。

假设我们有一段文本 ABRACADABRA，统计每个字符出现的频率如下：

字符 频率
A 5
B 2
R 2
C 1
D 1

根据上面的表格中的数据，我们就可以按照1.2章节中的步骤构建出一棵霍夫曼树了：

  1. 初始节点：[A:5, B:2, R:2, C:1, D:1]
  2. 取出频率最小的两个节点 C 和 D，合并成新节点 (C,D):2，队列变为 [A:5, B:2, R:2, (C,D):2]
  3. 取出频率最小的两个节点 B 和 R，合并成新节点 (B,R):4，队列变为 [A:5, (B,R):4, (C,D):2]
  4. 取出频率最小的两个节点 (C,D) 和 (B,R)，合并成新节点 ((C,D),(B,R)):6，队列变为 [A:5, ((C,D),(B,R)):6]
  5. 取出频率最小的两个节点 A 和 ((C,D),(B,R))，合并成根节点 (A,((C,D),(B,R))):11

在构建好霍夫曼树之后，我们可以通过遍历树来生成每个字符的霍夫曼编码。

  • 从根节点开始，向左子树遍历一步时，编码后面添加 0；向右子树遍历一步时，编码后面添加 1。
  • 当到达叶子节点时，记录该字符的编码。
image-20250220163014410

根据上述霍夫曼树，每个字符生成的霍夫曼编码如下：

字符 霍夫曼编码
A 0
B 110
R 111
C 100
D 101

对于文本 ABRACADABRA，编码后的二进制字符串为 01001010110011101001010。

2.2 解码

解码过程需要使用与编码过程相同的霍夫曼树，因此需要重新构建霍夫曼树。构建方法与编码过程中的步骤1.2章节相同。

从霍夫曼树的根节点开始，根据二进制编码的每一位，向左（0）或向右（1）遍历树。当到达叶子节点时，记录该叶子节点对应的字符，并回到根节点继续解码。

对于编码后的二进制字符串 01101110100010101101110，解码过程如下：

  1. 从根节点开始，第一位是 0，向左遍历到叶子节点 A，记录字符 A，回到根节点。
  2. 下三位是 110，向右、向右、向左遍历到叶子节点 B，记录字符 B，回到根节点。
  3. 下三位是 111，向右、向右、向右遍历到叶子节点 R，记录字符 R，回到根节点。
  4. 下一位是 0，向左遍历到叶子节点 A，记录字符 A，回到根节点。
  5. 下三位是 100，向右、向左、向左遍历到叶子节点 C，记录字符 C，回到根节点。
  6. 下一位是 0，向左遍历到叶子节点 A，记录字符 A，回到根节点。
  7. 下三位是 101，向右、向左、向右遍历到叶子节点 D，记录字符 D，回到根节点。
  8. 下一位是 0，向左遍历到叶子节点 A，记录字符 A，回到根节点。
  9. 下三位是 110，向右、向右、向左遍历到叶子节点 B，记录字符 B，回到根节点。
  10. 下三位是 111，向右、向右、向右遍历到叶子节点 R，记录字符 R，回到根节点。
  11. 最后一位是 0，向左遍历到叶子节点 A，记录字符 A，回到根节点。
  12. 最终解码得到原始文本 ABRACADABRA。

3. 霍夫曼树的CPP实现

3.1 定义霍夫曼树节点

1
2
3
4
5
6
7
8
struct HuffmanNode
{
    char data;
    int freq;   // 数据出现的频率（权值）
    HuffmanNode* left;
    HuffmanNode* right;
    HuffmanNode(char d, int f) : data(d), freq(f), left(nullptr), right(nullptr) {}
};
  • 成员变量：
    • char data：用于存储字符数据。
    • int freq：表示该字符数据出现的频率，也就是霍夫曼树中节点的权值。
    • HuffmanNode* left 和 HuffmanNode* right：分别是指向左子节点和右子节点的指针，用于构建树结构。
  • 构造函数：HuffmanNode(char d, int f) 是一个带参数的构造函数，用于初始化节点的字符数据 data、频率 freq，并将左右子节点指针初始化为 nullptr。

3.2 定义霍夫曼树类

HuffmanTree 类用于实现霍夫曼编码与解码的功能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 定义霍夫曼树
class HuffmanTree
{
public:
    HuffmanTree(const string& data);
    ~HuffmanTree();

    string encode();
    string decode(const string& encodeStr);
private:
    void buildTree(const string& data);
    bool encode(HuffmanNode* root, string& code, unordered_map<char, string>& huffmanCode);
    bool decode(HuffmanNode* root, int& index, const string& encodeStr, string& decodeStr);
    void clear(HuffmanNode* root);

private:
    string m_data;
    HuffmanNode* m_root;
    struct Compare
    {
        bool operator()(HuffmanNode* n1, HuffmanNode* n2)
        {
            return n1->freq > n2->freq;
        }
    };
};

下面将详细解释这个 HuffmanTree 类的设计与各个成员的作用。

公有成员函数

  • HuffmanTree(const string& data);

    • 功能：这是类的构造函数，接收一个字符串 data 作为参数。在构造对象时，它会调用 buildTree 函数根据输入的字符串构建霍夫曼树。
    • 参数：data 是待编码的原始字符串。

  • ~HuffmanTree();

    • 功能：这是类的析构函数，用于释放霍夫曼树所占用的内存。它会调用 clear 函数递归地删除树中的所有节点，防止内存泄漏。

  • string encode();

    • 功能：生成输入字符串的霍夫曼编码。它会遍历霍夫曼树，为每个字符生成对应的编码，并将原始字符串转换为霍夫曼编码字符串。
    • 返回值：返回一个字符串，该字符串是输入字符串的霍夫曼编码结果。

  • string decode(const string& encodeStr);

    • 功能：对给定的霍夫曼编码字符串进行解码。它会根据霍夫曼树，从编码字符串中还原出原始的字符串。
    • 参数：encodeStr 是待解码的霍夫曼编码字符串。
    • 返回值：返回解码后的原始字符串。

私有成员函数

  • void buildTree(const string& data);

    • 功能：根据输入的字符串 data 构建霍夫曼树。首先，它会统计字符串中每个字符出现的频率，然后使用优先队列（最小堆）来构建霍夫曼树。
    • 参数：data 是用于构建霍夫曼树的原始字符串。

  • bool encode(HuffmanNode* root, string& code, unordered_map<char, string>& huffmanCode);

    • 功能：这是一个辅助函数，用于递归地生成每个字符的霍夫曼编码。它从霍夫曼树的根节点开始遍历，向左遍历标记为 0，向右遍历标记为 1，直到到达叶子节点，将字符与对应的编码存储在 huffmanCode 中。
    • 参数：
      • root：当前遍历到的霍夫曼树节点。
      • code：当前生成的编码字符串。
      • huffmanCode：用于存储每个字符及其对应霍夫曼编码的映射。
    • 返回值：返回一个布尔值，表示是否成功生成编码。

  • bool decode(HuffmanNode* root, int& index, const string& encodeStr, string& decodeStr);

    • 功能：这是一个辅助函数，用于递归地对霍夫曼编码字符串进行解码。它从霍夫曼树的根节点开始，根据编码字符串中的 0 和 1 决定向左或向右遍历，直到到达叶子节点，将叶子节点的字符添加到解码结果字符串中。
    • 参数：
      • root：当前遍历到的霍夫曼树节点。
      • index：当前处理的编码字符串的索引。
      • encodeStr：待解码的霍夫曼编码字符串。
      • decodeStr：存储解码结果的字符串。
    • 返回值：返回一个布尔值，表示是否成功解码。

  • void clear(HuffmanNode* root);

    • 功能：这是一个递归函数，用于释放霍夫曼树所占用的内存。它从根节点开始，递归地删除每个节点及其子节点。
    • 参数：root 是当前要删除的子树的根节点。

私有成员变量

  • string m_data;

    • 功能：存储原始的待编码字符串，以便后续使用。

  • HuffmanNode* m_root;

    • 功能：指向霍夫曼树的根节点，用于后续的编码和解码操作。

私有结构体 Compare

1
2
3
4
5
6
7
struct Compare
{
    bool operator()(HuffmanNode* n1, HuffmanNode* n2)
    {
        return n1->freq > n2->freq;
    }
};

这是一个自定义的比较器，用于优先队列（最小堆）的排序。它定义了比较两个 HuffmanNode 节点的规则，使得频率较小的节点优先出队。

3.3 霍夫曼树API实现

构造和析构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
HuffmanTree::HuffmanTree(const string& data) : m_data(data)
{
    buildTree(data);
}

HuffmanTree::~HuffmanTree()
{
    clear(m_root);
    cout << "霍夫曼树已经被销毁!" << endl;
}

void HuffmanTree::clear(HuffmanNode* root)
{
    if (root == nullptr)
    {
        return;
    }
    clear(root->left);
    clear(root->right);
    delete root;
}

构建霍夫曼树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void HuffmanTree::buildTree(const string& data)
{
    unordered_map<char, int> freq;
    for (char ch : data)
    {
        freq[ch]++;
    }
    priority_queue<HuffmanNode*, vector<HuffmanNode*>, Compare> minHeap;
    for (const auto& item : freq)
    {
        minHeap.push(new HuffmanNode(item.first, item.second));
    }
    while (minHeap.size() > 1)
    {
        HuffmanNode* left = minHeap.top();
        minHeap.pop();
        HuffmanNode* right = minHeap.top();
        minHeap.pop();

        HuffmanNode* parent = new HuffmanNode(0, left->freq + right->freq);
        parent->left = left;
        parent->right = right;
        minHeap.push(parent);
    }
    m_root = minHeap.top();
    minHeap.pop();
}

  1. 统计字符频率

    1
    2
    3
    4
    5
    unordered_map<char, int> freq;
    for (char ch : data)
    {
        freq[ch]++;
    }
    • 首先，创建一个 unordered_map 类型的对象 freq，用于存储每个字符及其出现的频率。unordered_map 是 C++ 标准库中的哈希表容器，它可以高效地根据键（这里是字符）查找对应的值（这里是频率）。
    • 然后，使用范围 for 循环遍历输入字符串 data 中的每个字符 ch，并将该字符在 freq 中的频率加 1。如果该字符是第一次出现，unordered_map 会自动为其分配一个初始值为 0 的频率，并在后续加 1。

  2. 初始化最小堆

    1
    2
    3
    4
    5
    priority_queue<HuffmanNode*, vector<HuffmanNode*>, Compare> minHeap;
    for (const auto& item : freq)
    {
        minHeap.push(new HuffmanNode(item.first, item.second));
    }
    • 接着，创建一个优先队列 minHeap，它是一个最小堆。优先队列是一种特殊的队列，它可以根据元素的优先级（这里是节点的频率）对元素进行排序，使得优先级最高（频率最小）的元素总是位于队列的顶部。
    • priority_queue 的模板参数分别为：存储的元素类型 HuffmanNode*（指向霍夫曼节点的指针）、底层容器类型 vector<HuffmanNode*>（使用 vector 作为存储容器）和比较器类型 Compare（自定义的比较器，用于定义元素的优先级）。
    • 然后，遍历 freq 中的每个元素，为每个字符创建一个 HuffmanNode 节点，并将其插入到最小堆 minHeap 中。每个节点包含字符及其对应的频率。

  3. 构建霍夫曼树

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    while (minHeap.size() > 1)
    {
        HuffmanNode* left = minHeap.top();
        minHeap.pop();
        HuffmanNode* right = minHeap.top();
        minHeap.pop();

        HuffmanNode* parent = new HuffmanNode(0, left->freq + right->freq);
        parent->left = left;
        parent->right = right;
        minHeap.push(parent);
    }
    • 使用while循环，只要最小堆中的节点数量大于 1，就继续执行以下操作：
      • 从最小堆中取出频率最小的两个节点 left 和 right，并将它们从堆中移除。
      • 创建一个新的父节点 parent，该节点的字符值设为 0（因为它不是叶子节点，不代表具体字符），频率为 left 和 right 节点频率之和。
      • 将 left 和 right 分别作为 parent 节点的左右子节点。
      • 将新创建的父节点 parent 插入到最小堆中。

  4. 确定根节点

    1
    2
    m_root = minHeap.top();
    minHeap.pop();

    当最小堆中只剩下一个节点时，这个节点就是霍夫曼树的根节点。将该节点赋值给类的私有成员变量 m_root，并将其从最小堆中移除。

霍夫曼编码

在类中进行霍夫曼编码使用了两个函数:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
bool HuffmanTree::encode(HuffmanNode* root, string& code, unordered_map<char, string>& huffmanCode)
{
    if (root == nullptr)
    {
        return false;
    }
    if (root->data != '\0')
    {
        huffmanCode[root->data] = code;
        return true;
    }
    code += '0';
    bool leftSuccess = encode(root->left, code, huffmanCode);
    code.pop_back(); // 恢复 code 的值
    code += '1';
    bool rightSuccess = encode(root->right, code, huffmanCode);
    code.pop_back(); // 恢复 code 的值
    return leftSuccess && rightSuccess;
}

该函数是一个递归函数，用于生成霍夫曼树中每个叶子节点字符的霍夫曼编码。

参数：

  • root：当前递归处理的霍夫曼树节点。
  • code：当前正在生成的编码字符串，是一个引用类型，方便在递归过程中修改。
  • huffmanCode：用于存储每个字符及其对应的霍夫曼编码的哈希表，也是引用类型，方便在递归过程中更新。

代码解释：

1
2
3
4
if (root == nullptr)
{
    return false;
}

首先检查当前节点是否为空。如果为空，说明已经到达无效节点，返回 false。

1
2
3
4
5
if (root->data!= '\0')
{
    huffmanCode[root->data] = code;
    return true;
}

接着检查当前节点是否为叶子节点（即 root->data 不为 '\0'）。如果是叶子节点，将当前的编码字符串 code 存储到 huffmanCode 中，键为该叶子节点的字符 root->data，并返回 true。

1
2
3
code += '0';
bool leftSuccess = encode(root->left, code, huffmanCode);
code.pop_back(); // 恢复 code 的值

如果当前节点不是叶子节点，将 '0' 追加到 code 字符串中，表示向左子树遍历。然后递归调用 encode 函数处理左子树，将结果存储在 leftSuccess 中。递归返回后，使用 code.pop_back() 移除刚刚追加的 '0'，以恢复 code 到递归调用前的状态，以便后续处理右子树。

1
2
3
code += '1';
bool rightSuccess = encode(root->right, code, huffmanCode);
code.pop_back(); // 恢复 code 的值

类似地，将 '1' 追加到 code 字符串中，表示向右子树遍历。递归调用 encode 函数处理右子树，将结果存储在 rightSuccess 中。递归返回后，使用 code.pop_back() 移除刚刚追加的 '1'，恢复 code 的值。

1
return leftSuccess && rightSuccess;

最后返回 leftSuccess 和 rightSuccess 的逻辑与结果，表示左右子树的编码是否都成功。

第二个函数用于对整个数据串进行霍夫曼编码，并输出每个字符的霍夫曼编码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
string HuffmanTree::encode()
{
    string code;
    string encodeStr = string();
    unordered_map<char, string> huffmanCode;
    // 编码数据
    bool flag = encode(m_root, code, huffmanCode);
    if (flag)
    {
        for (char ch : m_data)
        {
            encodeStr += huffmanCode[ch];
        }
        cout << "数据串中各个字符的霍夫曼编码为: " << endl;
        for (const auto& item : huffmanCode)
        {
            cout << item.first << " : " << item.second << endl;
        }
    }
    return encodeStr;
}

霍夫曼解码

霍夫曼编码的解码在类中也是通过两个函数来实现，先看第一个:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
bool HuffmanTree::decode(HuffmanNode* root, int& index, const string& encodeStr, string& decodeStr)
{
    if (root == nullptr || index >= (int)encodeStr.size())
    {
        return false;
    }
    // 叶子节点, 将节点值保存起来
    if (root->data != '\0')
    {
        decodeStr += root->data;
        return true;
    }
    index++;    // 将索引 index 加 1，指向下一个编码字符，以便继续处理编码字符串
    if (encodeStr[index] == '0')
    {
        return decode(root->left, index, encodeStr, decodeStr);
    }
    else
    {
        return decode(root->right, index, encodeStr, decodeStr);
    }
}


该函数是一个递归函数，用于根据霍夫曼树对编码字符串中的一个字符进行解码。

参数：

  • root：当前递归处理的霍夫曼树节点。
  • index：编码字符串 encodeStr 的当前索引，是一个引用类型，方便在递归过程中修改。
  • encodeStr：待解码的编码字符串。
  • decodeStr：存储解码结果的字符串，也是引用类型，方便在递归过程中更新。

第二个函数用于对整个编码字符串进行解码：

1
2
3
4
5
6
7
8
9
10
11
12
13
string HuffmanTree::decode(const string& encodeStr)
{
    int index = -1;
    string decodeStr;
    while (index < (int)encodeStr.size() - 1)
    {
        if (!decode(m_root, index, encodeStr, decodeStr))
        {
            return string(); // 解码失败
        }
    }
    return decodeStr; // 解码成功
}

使用 while 循环遍历编码字符串，只要索引 index 小于编码字符串长度减 1，就继续解码。每次调用 decode 函数对一个字符进行解码，如果解码失败（decode 函数返回 false），则返回一个空字符串表示解码失败。

3.4 测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int main()
{
    string data = "wo ai da bing da bing shi ge da hao ren!";
    //string data = "ABRACADABRA";
    // 构建霍夫曼树
    HuffmanTree hfTree(data);
    // 生成霍夫曼编码
    string encodeStr = hfTree.encode();
    cout << "数据串的霍夫曼编码: " << encodeStr << endl;
    // 解码数据
    string decodeStr = hfTree.decode(encodeStr);
    cout << "解码之后的字符串: " << decodeStr << endl;
    return 0;
}

终端输出的结果如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
数据串中各个字符的霍夫曼编码为:
! : 00000
a : 011
i : 010
s : 00001
w : 00100
o : 0001
b : 0011
r : 00101
  : 10
d : 1100
g : 1101
n : 1110
h : 11110
e : 11111
数据串的霍夫曼编码: 0010000011001101010110001110001101011101101101100011100011010111011011000001111100101011011111110110001110111100110001100010111111111000000
解码之后的字符串: wo ai da bing da bing shi ge da hao ren!
霍夫曼树已经被销毁!