1. 进制

进制也就是进位制，是人们规定的一种进位方法。对于任何一种进制，比如 X 进制，就表示某一位置上的数运算时是逢 X 进一位。十进制是逢十进一，十六进制是逢十六进一，二进制就是逢二进一，以此类推，x 进制就是逢 x 进位。

十进制	二进制	八进制	十六进制
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A/a
11	1011	13	B/b
12	1100	14	C/c
13	1101	15	D/d
14	1110	16	E/e
15	1111	17	F/f
16	10000	20	10

1.1 二进制

二进制是计算技术中广泛采用的一种数制。二进制数据是用0和1两个数码来表示的数。它的基数为2，进位规则是 逢二进一，借位规则是借一当二。

当前的计算机系统使用的基本上是二进制系统，数据在计算机中主要是以补码的形式存储的。

术语	含义
`bit`(比特)	一个二进制代表一位，一个位只能表示0或1两种状态。数据传输是习惯以“位”（bit）为单位。
`Byte`(字节)	一个字节为8个二进制，称为8位，计算机中存储的最小单位是字节。数据存储是习惯以“字节”（Byte）为单位。
`WORD`(双字节)	2个字节，16位
`DWORD`	两个WORD，4个字节，32位
`1b`	1bit，1位
`1B`	1Byte，1字节，8位，1B = 8b, 1Byte = 8bit
`1k，1K`	1024
`1M`(1兆)	1024k, 1024*1024
`1G`	1024M
`1T`	1024G
`1Kb`(千位)	1024bit，1024位
`1KB`(千字节)	1024Byte，1024字节
`1Mb`(兆位)	1024Kb = 1024 * 1024bit
`1MB`(兆字节)	1024KB = 1024 * 1024Byte

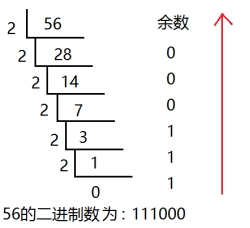
十进制转化二进制的方法：用十进制数除以2，分别取余数和商数，商数为0的时候，将余数倒着数就是转化后的结果。

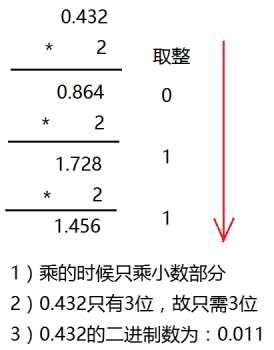
十进制的小数转换成二进制：小数部分和2相乘，取整数，不足1取0，每次相乘都是小数部分，顺序看取整后的数就是转化后的结果。

1.2 八进制

八进制，Octal，缩写OCT或O，一种以8为基数的计数法，采用0，1，2，3，4，5，6，7八个数字，逢八进1。一些编程语言中常常以数字0开始表明该数字是八进制。

八进制的数和二进制数可以按位对应（八进制一位对应二进制三位），它们之间的转换在计算机语言中也很常见，对应关系如下表：

`八进制`	`0`	`1`	`2`	`3`	`4`	`5`	`6`	`7`
二进制	000	001	010	011	100	101	110	111

十进制转化八进制的方法：

用十进制数除以8，分别取余数和商数，商数为0的时候，将余数倒着数就是转化后的结果。

1.3 十六进制

十六进制（英文名称：Hexadecimal），同我们日常生活中的表示法不一样，它由 0~9，A~F(a~f) 组成，字母不区分大小写。与10进制的对应关系是：0~9对应0~9，A~F(a~f)对应10~15。

十六进制的数和二进制数可以按位对应（十六进制一位对应二进制四位），它们之间的转换也很常见，对应关系如下表：

`十六进制`	`0`	`1`	`2`	`3`	`4`	`5`	`6`	`7`
二进制	0000	0001	0010	0011	0100	0101	0110	0111
`十六进制`	`8`	`9`	`A/a`	`B/b`	`C/c`	`D/d`	`E/e`	`F/f`
二进制	1000	1001	1010	1011	1100	1101	1110	1111

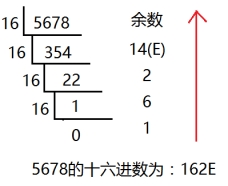
十进制转化十六进制的方法：

用十进制数除以16，分别取余数和商数，商数为0的时候，将余数倒着数就是转化后的结果。

1.4 进制数的表示

进制	描述
二进制	C语言不能直接书写二进制数
八进制	以数字`0`开头，如：0123、0765
十进制	以数字 `1-9` 开头，如：123、250
十六进制	以 `0x` 开头，如：0x123、0xfab

#include <stdio.h>
int main()
{
	int a = 123;        //十进制方式赋值
	int b = 0123;       //八进制方式赋值， 以数字0开头
	int c = 0xABC;      //十六进制方式赋值

	// 在printf中输出一个十进制数用 %d，八进制用 %o，十六进制用 %x
	printf("十进制：%d\n", a);
	printf("八进制：%o\n", b);	// %o,为字母o,不是数字
	printf("十六进制：%x\n", c);

	return 0;
}

程序输出的结果为:

1
2
3

十进制：123
八进制：123
十六进制：abc

2. 存储数据的方式

2.1 原码

所谓原码顾名思义就是数据的原始二进制码，一个数的原码有如下特点：

最高位做为符号位，0 表示正，1 表示负
其它数值部分就是数值本身绝对值的二进制数
负数的原码是在其绝对值的基础上，最高位变为1

下面使用 1字节的大小数值对原码进行描述：

十进制数	原码
+15	`0`000 `1111`
-15	`1`000 `1111`
+0	`0`000 0000
-0	`1`000 0000

原码表示法简单易懂，与带符号数本身转换方便，只要符号还原即可，但当两个正数相减或不同符号数相加时，必须比较两个数哪个绝对值大，才能决定谁减谁，才能确定结果是正还是负，所以原码不便于加减运算。

2.2 反码

反码是一种二进制数的表示方式，它有如下两个特点：

正数的反码和原码相同
负数的反码是将原码中的1变为0，0变为1（符号位不动）。

具体而言，对于一个 n 位的二进制数，如果是正数，则它的反码和原码相同；如果是负数，则它的反码是将原码中除了符号位以外的其它位取反。

十进制数	反码
+15	0000 1111
-15	1111 0000
+0	0000 0000
-0	1111 1111

使用反码进行加减运算其实也不方便，通常用来作为求补码的中间过渡。

2.3 补码

在计算机系统中，数值一律都是采用补码来存储的。补码的特点如下：

对于正数，原码、反码、补码相同
对于负数，其补码为它的反码加 1
补码符号位不动，其他位求反，最后整个数加1，得到原码

十进制数	补码
+15	0000 1111
-15	1111 0001
+0	0000 0000
-0	0000 0000

#include <stdio.h>
int main()
{
	int  a = -15;
	printf("%x\n", a);
	return 0;
}

上面代码输出的结果为 fffffff1，下面一起来推导一下：

fffffff1对应的二进制：1111 1111 1111 1111 1111 1111 1111 0001
符号位不变，其它取反：1000 0000 0000 0000 0000 0000 0000 1110
再加 1，1000 0000 0000 0000 0000 0000 0000 1111 最高位 1 代表负数，就是-15

2.4 补码的意义

下面我们来举几个例子，用以说明补码存在的意义：

示例1：用 8 位二进制数分别表示 +0 和 -0

十进制数原码反码

+0 0000 0000 0000 0000

-0 1000 0000 1111 1111

通过上表可以发现：不管以原码方式存储，还是以反码方式存储，0 也有两种表示形式。为什么同样一个0要有两种不同的表示方法呢？

但是如果以补码方式存储，补码统一了零的编码：

十进制数补码

+0 0000 0000

-0 0000 0000

基于之前对补码的描述可以得到如下公式：-0的补码 = -0反码 + 1，也就是1111 1111 + 1 = 1 0000 0000，由于约定只用 8 位（1个字节，1Byte）描述，最高位1丢弃，变为0000 0000，此时关于 0 的二进制存储就可以统一了。
示例2：计算 9-6 的结果

以原码方式相加，先看这两个数字对应的原码：

十进制数 原码

9 0000 1001

-6 1000 0110

二进制的0000 1111对应十进制的15，并且二进制数的符号位为1，也就是意味着结果是一个负数即：-15，很显然这个结果是不正确的。

我们可以以补码方式来计算这两个数的和，下表为这两个数的补码：

十进制数补码

9 0000 1001

-6 1111 1010

由于约定的是8位存储，所以最高位的 1 溢出，剩余8位二进制0000 0011表示的是3，正确。